Volcano-induced regime shifts in millennial tree-ring chronologies from Northeastern North America

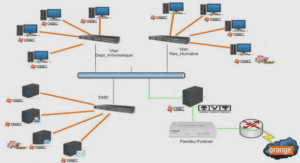
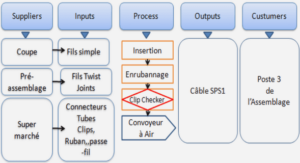
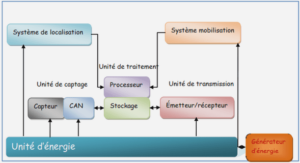
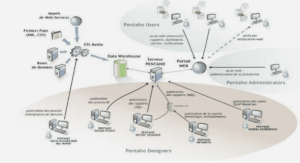
Studyarea

   The study area is located in the northern taiga of Quebec, Canada, between latitudes 53°50′ N and 54°35′ N and longitudes 70°15′ Wand 72°25′ W (Fig. 1). This are a is situated at the transition between the spruce-lichen woodland and the foresttundra and is characterized by a continental subarctic climate with short mild summers and long cold winters. The vegetation of the region reflects mostly the topography and the past fue history. Forests are strongly dominated by black spruce (Picea mariana (Mill.) BSP.), which is weIl adapted to various fire frequencies. Its semi-serotinuous cones shed seeds after fues, thus aIlowing rapid post-fue recovery, while its ability to form layers (i.e. to propagate vegetatively through the rooting of the lower branches that are touching the ground) al10ws stands to persist in the absence of fues (Black & Bliss 1980). Black spruce canopy height and density vary according to the time since the last fire, the severity of the fire and the topographie position of a given stand (Morneau & Payette 1989; Payette 1993; Lavoie & Sirois 1998; Girard, Payette & Gagnon 2008). Other less abundant tree species inc1ude balsam fIT (Abies balsamea L.) and tamarack (Larix laricina (Du Roi) K. Koch). The study area is located in a remote region where significant human influence IS sparse and only recent (last 40 years). Lakes of various sizes are extremely abundant, covering about 25% of the landscape. A portion of the littoral zone of each of the five lakes was selected for this study (Fig. 1, Table 1) according to the criteria developed by Arseneault et al. (2013) in order to identify sites of high potential for developing millennial tree-ring elu·onologies. The selected littoral segments possess features that maximize L WD recruitment (an abrupt forest-lake interface on the leeward side of the lake and an old-growth riparian forest) and L WD preservation (presence, near the shoreline, of a talus at least 1 m deep and, on its bottom, of fine sediments).

LWD stocks and dating

   The five sites were exhaustively sampled during several summer field campaigns between 2005 and 20 Il. Any exposed (i.e. laying on the bottom of the lake) or buried logs with a diameter equal or greater than 4 cm, which makes dendrochronological dating possible, were collected by a diver aided by two-three assistants, as described by Arseneault et al. (2013). Most logs were pulled to the shore, although a few heavy or stuck logs were partially eleared of sediments,measured and eut with a hand saw in the water. Buried specimens were located as loose sediments can be systematically probed by hand. Only L WD pieces buried in less than abo ut 20 cm of sediments could be extracted. Once on the shore, L WD pieces were mapped with a total station and their length and maximum diameter were measured in order to calcu\ate the LWD number and volume per 100 m ofshoreline,which are two metrics that characterize L WD stocks. The volume of each L WD piece was estimated as the volume of a cylinder multiplied by a form factor of 0.6. The form factor was based on more detailed measurements on a subset of 1626 L WD pieces from this study (i.e. minimum and maximum diameters and their position on each L WD piece). L WD specimens were also examined to detect the presence of charcoal on the trunk and the bran ch tips and the presence of main roots still connected or not. A stem cross-section was sampled from each L WD piece so as to maximize the number of measurable tree-rings for dendrochronological dating. In the lab, tree species were identified from wood anatomy (Hoadley 1990). Two radii were then scanned at 6400 DPI on each cross-section of spruce and fIT in order to measure tree-ring widths using the OSM3 software (SCIEM, Austria).lndividual series (i.e. average oftwo radii) were crossdated to the calendar year using local master chronologies as a reference (Arseneault et al. 2013) and sequences of light rings as an additional dating tool (Arseneault & Payette 1998). Crossdating was performed using COFECHA (Holmes 1983) and PAST4 (SCIEM, Austria) software. AlI floating chronologies older than the master chronology and comprising at least two tree-ring series of different L WD pieces, not necessarily from the same lake, were AMS (Accelerator Mass Spectrometry) radiocarbon dated. To do this, wood samples from the Îlmermost tree-rings of selected L WD pieces were sent to the Centre for Northern Studies (CEN) radiochronology laboratory (Université Laval, QC, Canada). Conventional radiocarbon ages were calibrated using CALIB 6.0  (Stuiver & Reimer 1993) and the IntCalO9 calibration curve.

L WD residence time and losses

   To determine the residence time in the lake of each L WD piece that could be crossdated to the calendar year or into a floating chronology, we estimated its recruitment date in the water from its outermost tree-ring date (hereafter « recruitment date »). The residence time was then determined as the time since the L WD recruitment (2012 minus recruitment date), even if this measure can be overestimated by a few years to a few decades due to the decomposition of outermost tree-rings. Similarly, the pith date of each L WD piece was used to estimate the date at which the corresponding former tree in ,the riparian forest had reached the height needed to develop an upper stem portion that later became recruited and conserved as a L WD piece (hereafter « establishment date »). To quantify the rate at which L WD pieces are lost from the littoral stocks by abiotic and biotic decomposition and burial, we identified distinct reference time intervals of negligible losses for exposed and buried specimens. First, the cumulative numbers of exposed and buried L WD samples were plotted separately according to residence time. Samples of aU lakes were plotted together in order to smooth out the impact of local disturbances (see Fig. 3a). Second, in the range of observed residence times, for each sequential time interval of 400 years lagged backward in time by 1 year, a linear regression model was fitted on the exposed and buried series until at least two L WD specimens could be included (the number of available specimens decreases backward in time). The successive slopes ofthese regression models aUow the comparison among time intervals as their values depend on the L WD recruitment into the exposed or buried groups during the corresponding time interval and on the cumulated losses. Higher recruitment rates would produce more negative slopes and higher losses would produce less negative slopes. With constant recruitment and no losses, the slopes would be constant. Third, for the exposed and buried series, the time interval with the more negative slope was considered as a reference state with no losses as it displayed a very good linear fit to the data (see Fig. 3a). lndeed, exposed specimens reside for some tune in water before being lost through decomposition or superficial burial, whereas buried specimens, after the tune needed for burial, reside for sorne time in superficial sediments before being lost through decomposition or deep burial (i.e. at depth greater than 20 cm). Last, assuming that recruitment of exposed and buried specimens is approximately constant through time when several lakes are averaged, the percentage of L WD losses for each 400 years time interval and each burial category was ca1culated as: [Lasses = 100 – (Si / Srej) * 100]. In the equation, Si is the slope of the regression on the residence time interval of 400 years centered in year i and Srejrefers to the corresponding reference slope. In addition, the proportion of the exposed L WD pieces that has been eventually buried relative to the proportion that has been lost through decomposition before burial was estimated from the ratio of the two reference slopes (buried over exposed). We also used the slopes of the most recent time intervals of each burial category to compute the average rate of L WD recruitment across ail studied lakes (number of LWD pieces per 100 years per 100 m ofshoreline computed as the summation of the 2 slopes x 100 years x 100 m, divided by a total of3330 m ofsampled shoreline).

Table des matières

INTRODUCTION GÉNÉRALE
CHAPITRE 1 STOCKS ET FLUX MILLÉNAIRES DE GROS DÉBRIS LIGNEUX DAN DES LACS DE LA TAÏGA NORD-AMÉRICAINE 
1.1 Résumé en français du premier article
1.2 Millennial stocks and fluxes of large woody debris in lakes of the North American taiga
1.2.1 Summary
1.2.2 Introduction
1.2.3 Materials and methods
1.2.4 Results
1.2.5 Discussion
1.2.6 Acknowledgments
1.2.7 Data Accessibility
1.2.8 References
1.2.9 Tables
1.2.10 Figures
1.2.11 Supporting information
CHAPITRE II DYNAMIQUES MILLÉNAIRES DES FORÊTS DE LA TAÏGA DE L’EST CANADIEN SOUS L’INFLUENCE DES INCENDIES
2.1 Résumé en français du deuxième article
2.2 Millennial disturbance-driven forest stand dynamics in the Eastern Canadian taiga reconstructed from subfossillogs
2.2.1 Summary
2.2.2 Introduction
2.2.3 Materials and methods
2.2.4 Results
2.2.5 Discussion
2.2.6 Acknowledgments
2.2.7 Data Accessibility
2.2.8 References
2.2.9 Tables
2.2.10 Figures
2.2.11 Supporting information
CHAPITRE III RECONSTITUTION DENDROCHRONOLOGIQUE DES TEMPÉRATURES ESTIVALES DU DERNIER MILLÉNAIRE DANS LA TAÏGA DE L’EST DE L’AMÉRIQUE DU NORD
3.1 Résumé en français du troisième article
3.2 Volcano-induced regime shifts in millennial tree-ring chronologies from Northeastern North America
3.2.1 Abstract
3.2.2 Significance Statement
3.2.3 Introduction
3.2.4 Results and Discussion
3.2.5 Methods
3.2.6 Acknowledgments
3.2.7 References
3.2.8 Tables
3.2.9 Figures
3.2.10 Supporting information
CONCLUSION
RÉFÉRENCES BIBLIOGRAPHIQUES

Télécharger le rapport complet