VIDEO COMPRESSION AND TRANSMISSION 

A MAXIMUM LIKELIHOOD APPROACH TO VIDEO ERROR CORRECTION APPLIED TO H.264 DECODING

Typical  Video Communication System

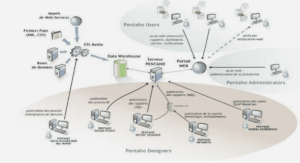
Each input picture passes through the video encoder, where at least one Network Abstraction Layer Unit (NALU) is created. Spliting each picture into multiple NALUs prevents the loss of entire pictures when packets are discarded due to network congestion. It is assumed that the communication protocol headers are added by the video encoder. The NALUs are then sent to the channel encoder, where they will be readied for transmission over an unreliable network. Upon reception, the protected NALUs are handled by the channel decoder, where either hard and/or soft information is sent to the communication protocol stack. The resulting RTP packet is then processed at the video application control layer and checked from transmission errors. The units that fail the error detection test are discarded, and those that pass the test move on to the video decoder. The video decoder then reconstructs the picture with the intact information, and conceals any missing information.

Proposed Video Communication System

  The typical communication system shown in the previous section needs to be modified if we are to exploit the corrupted packets. Figure 1.2 presents the modified system, where corrupted units that belong to the VCL are sent to a video error correction module.In this system, the error detection test is still required, as intact packets can simply be decoded. However, corrupted packets are not discarded. They are sent to a maximum likelihood error system where corrupted packets are discarded correction module where the corrupted information is transformed to create the most likely sequence of information. The output of the process is then passed to the video decoder, where normal reconstruction can take place. Because non-VCL units need to be correctly received,error correction is only applied to VCL units. With the proposed approach, the reconstructed picture is expected to resemble more closely the coded picture than with a typical system. Furthermore, this will also keep both ends of the system better synchronized, reducing the drifting effects introduced by the loss of packets.

Decoding time

  While conducting the second experiment, we also collected the decoding time of all four approaches for all the simulations we ran as a way to measure the complexity of the different approaches. The simulations were conducted on an iMac equipped with a 3.4 GHz Intel i7 processor, 8 Gb of 1333 DDR3 RAM running OS X 10.7. Our decoder was implemented using the C++ programming language, and compiled favoring execution speed over program size. Our implementation of the STBMA+PDE algorithm uses a maximum of 30 iterations in the PDE step. Table 5.8 summarizes the average decoding time per frame for all 9 sequences since the tests sequences share similar resolutions. The decoding times are in milliseconds per frame, and they are separated by channel SNR and QP since the amount of errors and the stream quality both affect the decoding and concealment time.

Concealment and correction comparison

 The average PSNR of the frames containing corrupted slices are presented in Tables 5.1, 5.2, and 5.3. Columns 2, 3, and 4 refer to the experiments using a channel SNR of 4 dB, while columns 5 to 7 refer to the experiments using a channel SNR of 5 dB. The differences between the results obtained with JM 16.0 and those obtained with STBMA+PDE and SO-MLD appear between parentheses. The results indicate that SO-MLD outperforms JM 16.0 in all cases, with the exception of the opening-ceremony, and whale-show sequences. In both cases, the coding behavior is difficult to predict, resulting in an increase in false positive, as well as false negative, detections. Moreover, the results also show that on average, SO-MLD performs better than STBMA+PDE for the vast majority of the sequences studied. Overall, STBMA+PDE’s PSNR gain is 0.76 dB over JM 16.0 at a channel SNR of 4 dB, and 1.77 dB at a channel SNR of 5 dB, while SOMLD’s gain is 1.42 dB at a channel SNR of 4 dB, and 1.96 dB at a channel SNR of 5 dB. Both increases are an indication that exploiting corrupted slices yields better results.

Table des matières

INTRODUCTION 
CHAPTER 1 VIDEO COMPRESSION AND TRANSMISSION 
1.1 Typical Video Communication System 
1.2 Proposed Video Communication System 
1.3 Network Abstraction Layer Units
1.4 Video Coding Layer Units
1.5 Exponential-Golomb Codes 
CHAPTER 2 LITERATURE REVIEW
2.1 Video Error Concealment
2.1.1 Spatial Error Concealment
2.1.2 Temporal Error Concealment
2.1.3 Hybrid Error Concealment
2.1.4 Concealment Order
2.2 Video Error Correction 
2.2.1 List Decoding
2.2.2 Joint Source-Channel Decoding
2.2.3 Discussion
CHAPTER 3 MAXIMUM LIKELIHOOD VIDEO ERROR CORRECTION 
3.1 Slice-Level Error Correction
3.1.1 Channel Decoding
3.1.2 Source Decoding
3.2 Syntax-Element-Level Error Correction 
CHAPTER 4 H.264 BASELINE PROFILE VIDEO ERROR CORRECTION
4.1 Slice Header 
4.1.1 first_mb_in_slice
4.1.2 slice_type
4.1.3 pic_parameter_set_id
4.1.4 frame_num and pic_order_cnt_lsb
4.2 Slice Data
4.2.1 mb_type
4.2.2 mb_skip_run
4.2.3 Intra4x4PredMode
4.2.4 intra_chroma_pred_mode
4.2.5 sub_mb_type
4.2.6 mvd_l0
4.2.7 coded_block_pattern
4.3 Early Termination
CHAPTER 5 EXPERIMENTAL RESULTS
5.1 Experimental Setup
5.2 Concealment and correction comparison 
5.3 Hard-output and soft-output comparison
5.4 Decoding time
5.5 Current limitations
CHAPTER 6 CONTRIBUTIONS .
CONCLUSION 
ANNEX I ERROR RESILIENCY COST
ANNEX II RANDOM TAIL ASSUMPTION 
ANNEX III EXPERIMENTAL TEST SET 
ANNEX IV MATLAB NETWORK SIMULATOR
ANNEX V EXPERIMENTAL OBSERVATIONS
BIBLIOGRAPHY

Télécharger le rapport complet