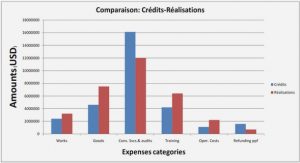
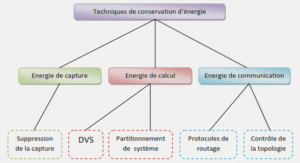
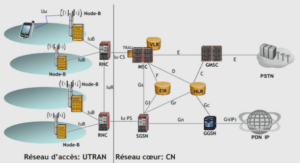
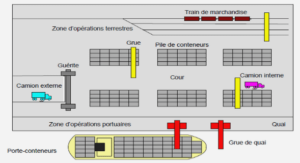
We spend most of our time making decisions. Perhaps we all are familiar with the difficulties that arise when looking for the best decision. Making the best decision often amounts to solve an optimization problem. This can be a hard task for several reasons: in some cases good solutions to a problem are counter-intuitive, in other cases finding them without appropriate methods is too time-consuming. The necessity of designing general paradigms to help the decision process has attracted the interest of many researchers, leading to the development of the Operations Research. This latter is a flourishing discipline at the intersection of mathematics and computer science, which provides several methods to solve optimization problems. Due to this dual nature, Operations Research has given rise to both applied and theoretical investigations. In this thesis we consider both aspects.
The first of our goals is to apply some well-established methods of the Operations Research to a problem arising in logistics. Logistics deals with the organization of transports at several stages. The recent technological advances and social changes have made logistics central in global economy. For instance, the availability of widely differing products at a low cost (made possible by a more and more automated mass production and by the relocation of the production) has generated an increase of good exchanges and commercial traffic in last years. To avoid loss of competitiveness and to limit the harmful effects of the traffic increase (e.g., pollution, congestion,. . . ), a topical research subject is the optimization of the routes of the transport vehicles.
In this thesis we consider the double traveling salesman problem with multiple stacks, in which the construction of optimal routes is severely constrained by the rules governing the disposition of the merchandise in a vehicle. In this problem, first some goods have to be picked up in one region. Subsequently they are delivered to demanding customers in another region, very far from the first one. For this transport, the items are positioned in stacks obeying the last-in-first-out rule for unloading. The double traveling salesman problem with multiple stacks is a combinatorial optimization problem. Many successful methods to tackle this kind of problems rely on the polyhedral approach introduced by Edmonds [54].
The idea behind the polyhedral approach is to associate the solutions to a combinatorial optimization problem with a set of points in a suitable space. Such a set of points can be associated to a geometrical object called polytope. A complete description of this polytope by means of linear inequalities can be used to solve the starting problem in practice. Unfortunately, complete descriptions of this type are unlikely to be found for hard problems.
This is why we often have to combine partial descriptions with integrality constraints in order to formulate the problem properly. Integer Programming is a research area which develops tools to solve such kind of formulations, called integer linear programs. A wellknown approach in Integer Programming is to seek an optimal solution by performing a dichotomic search and by exploiting the partial description in terms of linear inequalities to avoid a complete enumeration of all possible solutions. A method of this type is called branch-and-cut algorithm. The polyhedral approach and the branch-and-cut paradigm have proven to be very efficient in tackling hard combinatorial optimization problems.
A combinatorial optimization problem consists in minimizing (or maximizing) a function over a finite (but usually huge) set of elements, called feasible solutions to the problem. As an example, finding a shortest path linking two locations in a network can be seen as a combinatorial optimization problem. In fact, a shortest path problem in a network can be easily modeled using a weighted digraph. In general, the word “combinatorial” refers to the existence of an underlying abstract structure of finite cardinality (as the digraph of our example). Another well-known example is the Traveling Salesman Problem.
|
Table des matières
Introduction
1 General Definitions
1.1 Sets
1.2 Linear Algebra
1.2.1 Matrices
1.2.2 Vectors and Vector Spaces
1.2.3 Linear Functions
1.2.4 Linear Independence and Bases
1.2.5 Affine Spaces
1.2.6 Conic and Convex Combinations
1.3 Graphs
1.3.1 Undirected Graphs
1.3.2 Directed Graphs
1.4 Notions of Computational Complexity Theory
1.5 Polyhedral Theory
1.6 Combinatorial Optimization Problems and Integer Linear Programming
1.6.1 Polyhedral Approach
1.6.2 Cutting Plane Method
1.6.3 Branch-and-Cut Algorithm
1.6.4 Heuristics
2 The Double Traveling Salesman Problem with Multiple Stacks
2.1 Introducing the Double Traveling Salesman Problem with Multiple Stacks
2.2 The Double TSP with Multiple Stacks in Terms of Graphs
2.3 Links with Other Routing and Pickup and Delivery Problems
2.3.1 The Traveling Salesman Problem
2.3.2 Pickup and Delivery Problems
2.3.3 Pickup and Delivery Problems with Last-in-First-Out Constraints
2.4 State of the Art on the Double TSP with Multiple Stacks
2.4.1 Integer Linear Programming Formulations
2.4.2 Theoretical Results
2.4.3 Heuristic Approaches
2.4.4 Exact Methods
Conclusion
![]() Télécharger le rapport complet
Télécharger le rapport complet