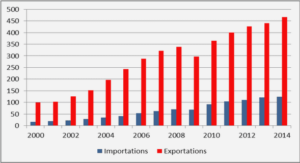
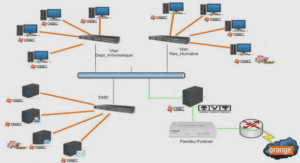
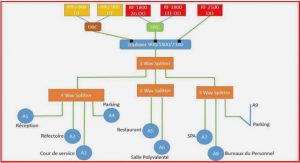
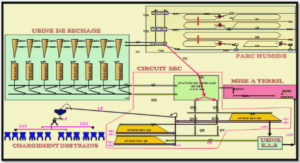
THE DISCRETE WAVELET TRANSFORM AND THE EMPIRICAL MODE DECOMPOSITION 

THE DISCRETE WAVELET TRANSFORM AND THE EMPIRICAL MODE DECOMPOSITION 

The discrete wavelet transform

The wavelet transform (Daubechies, 1988; Mallat, 1999) is a multi-resolution analysis of a signal that has the advantage of great ability to identify and extract signal details at several resolutions. For instance, the wavelet transform decomposes a signal into a number of frequency subbands. In the case of two dimensional (2D) signals –for example a digital image-, the series of wavelet subbands give a spatial view of the image details at various resolutions and orientations (horizontal, vertical, diagonal).

The empirical mode decomposition

The EMD is a general nonlinear, nonstationary signal processing method that was introduced by Huang et al., (1998). The major advantage of EMD is that the analysis is adaptive. In other words, the basis functions are derived directly from the signal itself. The key feature of the EMD is to decompose a signal into a sum of functions. Each of these functions (1) have the same numbers of zero crossings and extrema, and (2) is symmetric with respect to its local mean. These functions are called Intrinsic Mode Functions (IMF). The IMF are found at each scale going from fine to coarse by an iterative procedure called sifting algorithm. For a signal s(t), the EMD decomposition is performed as follows ( Liu, Xu, and Li, 2007):
a) find all the local maxima, M ,i =1,2,…, i and minima, m , k = 1,2,…, k in s(t),
b) compute by interpolation -for instance by cubic Spline- the upper and lower envelopes of the signal: M () ( ) t f M t M i = , and m() ( ) t f m t m i = , ,
c) compute the envelope mean e(t) as the average of the upper and lower envelopes: e() () () t = ( ) M t + m t 2 ,
d) compute the details as: d() () () t = s t − e t ,
e) check the properties of d(t):
• If d(t) meets the above conditions (1) and (2) given previously, compute the ith IMF as :
IMF() () t = d t and replace s(t) with the residual r() () () t = s t − IMF t ,
• If d(t) is not an IMF, then replace s(t) with the detail: s() () t = d t ,f) return to step (a) and iterate to step (e) until the residual r(t) satisfies a given stopping criteria.

The discrete wavelet transform in retina photographs processing

Lamard et al., (2007) introduced an algorithm based on the translation invariant wavelet transform and template matching to detect Retina microaneurisms. Then, they considered the horizontal and vertical sub-bands at several scales plus the approximation of the signal to extract features. Finally, specificity and sensitivity statistics are used to evaluate the classification system for different wavelet mothers and decomposition levels. The simulation results show that the best combination is obtained with the Haar wavelet and second level of decomposition with 96.18% specificity and 87.94% sensitivity. Khademi and Krishnan (2007) employed the 2-D version of Belkyns’s shift-invariant DWT (SIDWT) to classify normal against abnormal (exudates, large drusens, fine drusens, choroidal neovascularization, central vein and artery occlusion, arteriosclerotic retinopathy, histoplasmosis, hemi-central retinal vein occlusion) retina images. In order to capture texture directional features, normalized gray level co-occurrence matrices (GLCMs) are computed at 0◦ in HL, 90◦ in LH, 45◦, 135◦ in HH and 0◦, 45◦, 90◦ and 135◦ in the LL sub-band. Then, homogeneity and entropy statistics were computed from LH, HL, HH and LL sub-bands for each decomposition level. For instance, the decomposition level was set to four. Finally, linear discriminant analysis (LDA) is used as classifier in conjunction with the Leave One Out Method (LOOM). The obtained classification accuracy was 82.2%. In order to detect Microaneurysms in retina photographs, Quellec et al., (2008) employed 3- level wavelet decomposition and used genetic algorithms to find the best discriminative wavelet mother (Haar, biorthogonal, orthogonal) function and coefficients from HH, HL, and LH sub-bands.

Other approaches for retina digital image processing

Baroni et al., (2007) suggested a computer approach based on co-occurrence matrices for the analysis of retinal texture and artificial neural networks (ANN) to classify single retinal layers. The obtained accuracy was 79%, specificity about 71% and sensibility was 87%. Meier et al., (2007) used four approaches to extract features from retina to automatically classify glaucoma images. The first set of features is obtained by taking the pixel intensities as input to principal component analysis. The second features are obtained from Gabor texture filter responses. The third set of features is computed from the coefficients of the Fast Fourier Transform. The fourth set of features is obtained from the histogram of the intensity distribution of the image. Finally, support vector machines were employed for classification purpose. The performance of the classifications using one feature set only was 73% with the histogram features, 76% with Fast Fourier Transform coefficients, 80% with the Gabor textures and 83% with the pixel intensities. Franzco et al., (2008) used Fourier transform to evaluate the optical degradation of a retinal image of a cataractous eye. The experimental results showed that Fourier analysis of retinal images is significantly correlated with LOCS III (R-squared = 0.59) in grading cataract severity. In addition, it is found that Fourier analysis shows a comparable correlation with visual acuity (R-squared = 0.39) as LOCS III (R-squared = 0.44). They concluded that Fourier analysis is a useful automated method in grading of cataract severity; but it cannot determine the anatomic type of cataract. Lee et al., (2008) employed probabilistic boosting algorithm for nonhomogenous texture discrimination. In particular, the main purpose was to detect drusen in retina texture. They used morphological scale space analysis and grey level co-occurrence matrices (GLCM) to extract texture features. Using four different test samples, the detection rate of normal images varied between 81.3% and 92.2%, and the detection rate of abnormal images varied between 71.7% and 85.2%

The empirical mode decomposition in biomedical image processing

The Empirical Mode Decomposition (EMD) technique has been successfully applied in biomedical engineering problems. In particular, it has been largely employed in cardiovascular signal processing; including classification of EEG (Tafreshi et al., 2008), ECG denoising (Pan et al., 2007), ECG, BCG, PPG, and IPG processing (Pinheiro et al., 2011). The EMD has also been applied to two dimension signals. For instance, Nunes et al., (2003) applied the 2D-EMD to synthetic and brain magnetic resonance images to extract features at multiple spatial frequencies. The study showed the effectiveness of the EMD to represent images. They concluded that the 2D EMD offers a new and promising way to decompose images and extract texture features without parameter.
In late 2000s, the EMD has been employed in medical image processing. For instance, Qin et al., (2008) employed 2D-EMD to enhance medical images. Experiments show that good results are obtained by using 2D-EMD than using linear gray-level, transformation, piecewise linear gray-level transformation, logarithmic transformation, exponential transformation, and histogram equalization transformation. In particular, details of medical images were more definite and distinct after enhancement. McGonigle et al., (2010) employed a Multi-EMD approach to analyze signals obtained from functional neuroimages.
In particular, the purpose was to find which Intrinsic Mode Function (IMF) from each voxel should be used to represent the data at each scale. Finally, k-means clustering was performed on multi-EMD components to discover regions that behave synchronously at each temporal scale. They found that Multi-EMD based cluster analysis discriminate much better temporal scales than wavelet-based cluster analysis (WCA). McGonigle et al., (2010) concluded that Multi-EMD based clustering is a promising approach to explore functional brain imagery.
Liu et al., (2007) applied Bidimensional Empirical Mode Decomposition (BEMD) to the problem of biomedical images retrieval using k-means clustering. In other words, EMD was employed to analyze texture of images and the mean and standard deviation of the amplitude matrix, phase matrix and instantaneous frequency matrix of the Intrinsic Mode Functions (IMFs) and their Hilbert transformations. The experimental results show that retrieval results of Gabor features are higher than that of BEMD-based features. On the other hand, BEMD performs much better than wavelet-fractal based approach. Jai-Andaloussi et al., (2010) employed the BEMD to obtain characteristic signatures of images for Content Based Medical Image Retrieval (CBIR). Two approaches were considered. The first approach called BEMDGGD was based on the application of BEMD to medical images. Then, the distribution of coefficients derived from BIMF was characterized using Generalized Gaussian Density (GGD). In the second approach called BEMD-HHT, the Huang-Hilbert transform (HHT) was applied to each Bidimensional Empirical Mode Function (BIMF). Then, the mean and standard deviation were extracted from the amplitude matrix, phase matrix and instantaneous frequency matrix of each transformed (BIMF). Genetic algorithms were employed to generate adapted BIMF distance weights for each image in the database. The previous approaches were tested on the three databases including a diabetic retinopathy, a mammography and a faces database. The experimental results show that BEMD-GGD gives globally better results than BEMD-HHT. In addition, the retrieval efficiency is higher than 95% for some cases.

Table des matières

INTRODUCTION
CHAPTER 1 THE DISCRETE WAVELET TRANSFORM AND THE EMPIRICAL MODE DECOMPOSITION 
1.1 The discrete wavelet transform
1.2 The empirical mode decomposition
w(t) = sin(1000.t) + 3.sin(2000.t) + 5.sin(4000.t)
CHAPTER 2 HISTORICAL BACKGROUND 
2.1 The discrete wavelet transform in retina photographs processing
2.2 Other approaches for retina digital image processing
2.3 The empirical mode decomposition in biomedical image processing
CHAPTER 3 CONTRIBUTION AND METHODOLOGY
3.1 The contribution of our study
3.2 The proposed approach
3.3 Details of the proposed approach
3.3.1 Image processing
3.3.2 The mother wavelet
3.3.3 The empirical mode decomposition algorithm
3.3.3.1 Extrema location
3.3.3.2 Extrema interpolation
3.3.3.3 End effects
3.3.3.4 Mean envelop removal
3.3.3.5 Stopping criterion
3.3.4 Features extraction
3.3.5 The classifiers
3.3.5.1 Support vector machines
3.3.5.2 Quadratic discriminant analysis
3.3.5.3 The k-nearest neighbour algorithm
3.3.5.4 The probabilistic neural network
3.3.6 The principal component analysis
3.3.7 Performance measures
CHAPTER 4 DATA AND RESULTS 
4.1 Database
4.2 Experimental results
4.2.1 Discrete wavelet transform simulation results
4.2.2 Empirical mode decomposition simulation results
4.2.3 Principal component analysis based features results
4.2.4 Comparison of simulation results
CHAPTER 5 DISCUSSION OF THE OBTAINED RESULTS 
CONCLUSION

Télécharger le rapport complet