Smart Home and home automation applications

Exact approach

Exact solutions to the application placement problem can be achieved using integer linear programming (ILP) (Houidi, Louati et Zeghlache, 2008), (Yu et al., 2008), (Butt, Chowdhury et Boutaba, 2010).The integer linear programming (ILP) problem is a mathematical model where we maximize or minimize a linear function subject to linear constraints and in which some or all of the variables are integers. Integer linear programming (ILP) can be used to model the application component mapping and the communication edge mapping. Several algorithms try to solve the problem such as branch and bound, branch and cut, etc. Several solvers support these algorithms e.g. GLPK or CPLEX (Meindl et Templ, 2012). (Houidi et al., 2011) have addressed the virtual network allocation problem. To solve the problem, they have proposed an exact embedding algorithm that provides simultaneous node and link mappings in order to minimize the embedding cost for infrastructure providers while increasing the acceptance ratio of requests. For that, they have formulated the virtual network embedding problem as a mixed integer linear problem (MILP). Authors have expressed the embedding cost of a virtual network request as the sum of costs of allocated infrastructure resources in regard to the demands of the virtual network requests which is expressed as follows:

Where

represents the amount of bandwidth assigned from the infrastructure link ? to the virtual link between nodes ? and ?is the amount of bandwidth required at the virtual node ? , ?? and ?? are uniformly distributed variables. This proposal shows very encouraging results because it enables a simultaneous node and link mapping. However, in their objective function proposal, they have considered embedding cost as a linear function of the resource utilization which will result in suboptimal solutions mainly in utility environments where resources are not priced linearly to their processing power. Moreover, this solution has not considered different types of compute and network resources. (Botero et al., 2012) have proposed an exact cost optimal solution to the virtual network embedding problem. For that, they have expressed the cost in terms of energy consumption. Their proposed solution consolidates resources and minimizes the set of mapped equipment in order to gain energy by turning off the inactive servers. Authors have used Mixed Integer Linear Programming (MILP) to solve the virtual network embedding problem. Their objective function proposal aims to minimize the energy consumption by minimizing the set of inactive physical nodes and links that are activated after mapping a virtual network request. It is expressed as: ?? et ?(?, ?) are binary variables indicating respectively whether the node ? and the substrate link (?, ?) are activated after the mapping. This solution enables both node and link mapping and takes into consideration infrastructure specific constraints. However, their proposed solution differs from ours since they have expressed the cost in terms of energy consumption.

Heuristic

In cases where the computation time of an exact approach is not practical, heuristic-based approaches are adopted in order to achieve faster computation time needed. As we have discussed, heuristic solutions use a practical approach but are not guaranteed to be optimal. There is a great body of research work dealing with the application placement problem using proposed heuristic solutions. (Chowdhury, Rahman et Boutaba, 2012) have suggested a virtual embedding solution that minimizes the embedding cost. This solution proposal coordinates better node and link mapping based on linear programming relaxation. It solves a mixed integer linear programming (MILP) problem and the multicommodity flow (MCF) problem through relaxation methods. To do so, authors first perform the node mapping by introducing abstract nodes in the physical graph connected to a set of physical nodes for each virtual node. After that, they use the multicommodity flow (MCF) problem to map the virtual links considering that each link is a connected to a pair of abstract nodes.

The embedding problem is formulated with linear constraints on physical links and binary constraints on abstract links. The objective function is formulated as follows: Where ??(?, ?) and ??(?) are respectively the available capacity of a physical path and node, ? represents the assigned flow on the physical edge ?? for the virtual edge ? and ?(?) is the CPU capacity of the node ?. This solution proposal has shown promising results compared to other mapping algorithms. However, their cost objective function is fully linear to the resource utilization. Moreover, though their solution consists of a better coordination between the node and link mapping, the two phases are still done separately resulting in sub-optimal solutions. (Yu et al., 2008) have also researched the virtual network embedding problem. They have proposed the use of a greedy algorithm for the node mapping that greedily maximizes the resource utilization of the physical nodes. Then, they have considered two approaches for the link mapping, the unsplittable link mapping by adopting the k-shortest path algorithm and splittable link mapping by solving the multicommodity flow and problem. In the case where the multicommodity flow problem is unsolvable, the link mapping proposed algorithm reassigns the mapped nodes to the available ones. Their objective function aims to maximize the average revenue e.g. resource utilization and consists of:

Where ?? represents the graph of the virtual network, ??(??) is the bandwidth demand of the virtual link ?? and ???(??) is the CPU demand of the node ??. This solution proposal considers mapping nodes and links separately which will result in suboptimal solutions. Moreover, similar to previous approaches, the cost model is expressed in terms of resource utilization. In (Dubois et Casale, 2016), authors have proposed a heuristic approach that automates the application deployment decision while trying to minimize the spot prices and to maintain good performances. Authors have considered modeling applications as queuing networks of components. Their solution proposal consists first of choosing the minimum computational requirements for each application component. Next, it calculates the bidding price that minimizes the cost for each unit of rates and, based on it, decides which resources to rent and then considers the mapping of application components to the rented resources. Their optimization problem is formulated as follows: The objective function aims to minimize the sum of rental prices such that the mean response time should be lower than their respective maximums.

This solution proposal has shown promising results compared to other existing approaches. In addition, it has considered a pricing model adopted by the current Cloud providers which is not linear to the resource utilization. Nevertheless, this approach has only considered the node mapping in the formulation which leads to deployed applications with poor performance. (Wang, Zafer et Leung, 2017) have proposed non-LP approximation algorithms to solve the application placement problem in the mobile edge-computing context. The authors first 57 considered the case of a linear application graph and proposed an algorithm for finding its optimal solution and then considered the tree application graph case and propose online approximation algorithms. This solution proposal has considered both node and link assignment in the application placement problem. Their optimization objective is based on load balancing. gives the total cost of the resource of type ? requested by all application nodes that are assigned to node ? and ??(?) is the total cost of all assigned edges. Their objective function is expressed linearly to the resource utilization. This solution proposal is only limited to certain application topologies. Furthermore, the aim of the objective function is load balancing which is different from our approach. (Lischka et Karl, 2009), authors have proposed a solution based on subgraph isomorphism that maps the node and link mapping at the same stage. The isomorphism solution is well defined in graph theory and is about finding a subgraph fulfilling the demands in the physical infrastructure. However, subgraph isomorphism method is known to output sub-optimal solutions in most cases.

Table des matières

CHAPTER 1 INTRODUCTION
1.1 Context and motivation
1.2 Problem statement
1.3 Research questions
1.4 Objectives
1.5 Plan
CHAPTER 2 TECHNICAL BACKGROUND
2.1 Cloud computing and virtualization
2.1.1 Cloud computing
2.1.1.1 Definition
2.1.1.2 Models of Cloud Computing
2.1.1.3 Types of Cloud Computing
2.1.2 Virtualization
2.1.2.1 Types of virtualization
2.2 Smart Home and home automation applications
2.2.1 Smart Home architecture system
2.2.2 Smart Home existing solutions
2.2.2.1 Amazon IoT
2.2.2.2 Azure IoT Hub
2.2.3 Smart home applications requirements
2.2.3.1 Heterogeneity
2.2.3.2 Intra-application dependencies
2.2.3.3 Increase in traffic demand
2.2.3.4 Timing and location
Conclusion
CHAPTER 3 LITERATURE REVIEW
3.1 Application placement problem
3.1.1 Application placement algorithms
3.1.1.1 Exact approach
3.1.1.2 Heuristic
3.1.1.3 Metaheuristic
3.1.2 Comparison and discussion
3.1.2.1 Comparison
3.1.2.2 Discussion
Conclusion
CHAPTER 4 METHODOLOGY
4.1 Application virtualization platform requirements
4.1.1 R1: Modeling Smart Home applications
4.1.2 R2: Efficient mapping of application components to Cloud resources
4.1.3 R3: A mapping approach that maintains the required QoS
4.1.4 R4: Automatic deployment of distributed applications
4.2 System modeling
4.2.1 Application layer model
4.2.1.1 Resource requirements model
4.2.1.2 Illustrative example
4.2.2 Infrastructure layer model
4.2.3 Virtual layer model
4.3 Resource provisioning
4.3.1 Resource matching
4.3.2 Resource mapping
4.4 Mapping costs of Cloud resources
4.5 Problem formulation
4.6 OptiDep algorithm
4.7 Proposed architecture
4.7.1 Decision module
4.7.2 Deployment module
4.7.2.1 Architecture
4.7.2.2 Deployment module process
Conclusion
CHAPTER 5 SYSTEM IMPLEMENTATION AND EVALUATION RESULTS
5.1 System implementation
5.1.1 Decision module implementation
5.1.1.1 The I/O module
5.1.1.2 Graphical user interface
5.1.1.3 Mapping algorithm
5.1.1.4 Data collection module
5.1.2 Deployment module implementation
5.1.2.1 Overview
5.1.2.2 OpenStack
5.1.2.3 Testbed implementation
5.1.2.4 Pricing model
5.1.2.5 Example of a complex service deployment
5.2 Resource requirements model: Case study
5.2.1 Evaluation of compute and network requirements
5.2.1.1 Evaluation of the CPU requirements
5.2.1.2 Evaluation of memory requirements
5.2.1.3 Evaluation of bandwidth requirements
5.2.2 Analytical results of application dependencies
5.2.2.1 CPU
5.2.2.2 Memory
5.2.2.3 Bandwidth
5.2.3 Discussion
5.3 Evaluation results of the application placement algorithm
5.3.1 Simulation environment
5.3.2 Experiment objectives
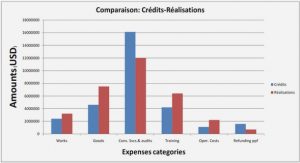
5.3.2.1 Cost
5.3.2.2 CPU utilization
5.3.2.3 Memory utilization
5.3.2.4 Acceptance ratio
5.3.2.5 Computation time
5.3.3 Reference algorithms for comparison
5.3.4 Evaluation method
5.3.5 Evaluation results
5.3.5.1 Cost
5.3.5.2 Resource utilization
5.3.5.3 Acceptance ratio
5.3.5.4 Computation time
5.3.6 Discussion
Conclusion
GENERAL CONCLUSION
APPENDIX I EXAMPLE OF A DEPLOYABLE STACK
APPENDIX II EXAMPLE OF A MASTER DEPLOYMENT TEMPLATE
APPENDIX III EXAMPLE OF A DEPLOYMENT TEMPLATE OF AN APPLICATION
COMPONENT
LIST OF REFERENCES

Télécharger le rapport complet