Proposition d’un cadre générique pour la résolution de problèmes combinatoires 

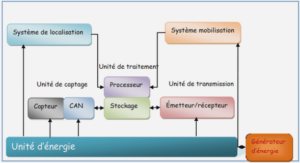
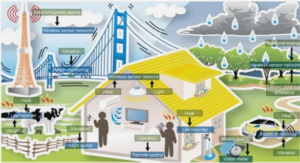
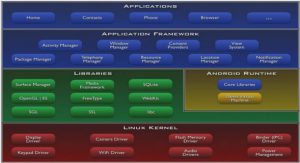
Télécharger le fichier pdf d’un mémoire de fin d’études

Modélisation mathématique des écoulements

Cette section vise à présenter les modèles mathématiques utilisés pour modéliser l’écoulement fluvial.
Dans ces travaux de thèse, les écoulements fluviaux d’intérêt sont en une dimension. L’avantage des modèles 1D est de pouvoir modéliser des grandes portions de rivières et de réseaux de rivières avec un temps de calcul raisonnable. Sur ces portions de rivières, on suppose que les variations des grandeurs hydrauliques sur une section en travers sont négligeables. Cette hypothèse est justifiée par le fait que l’on s’intéresse à la modélisation de grandes portions de rivières très larges et donc, à des écoulements à grande échelle.
Il convient tout de même de noter que ces modèles 1D ne permettent pas de modéliser des phénomènes 2D et 3D, comme par exemple les champs d’écoulement sur les plaines d’inondations.
Dans un premier temps, les géométries des rivières, ainsi que les notations associées à l’écoulement sont présentées. Les équations de Navier-Stokes (voir e.g. Batchelor [2000]) dans le cadre particulier d’écoulements à surface libre, dont fait partie l’écoulement fluvial, sont présentées pour poser la base de la modélisation de l’écoulement en question. C’est à partir de ce modèle que les modèles 1D sont par la suite dérivés.
Le système de Saint-Venant est le premier système 1D qui est présenté, voir e.g. Thual [2010]. Ces équations sont dérivées en intégrant celles de Navier-Stokes sur la section en travers et en utilisant l’hypothèse d’ondes longues pour traduire l’aspect « eau peu profonde » de l’écoulement.
Finalement, l’équation de l’onde diffusante est introduite, voir e.g. Lighthill et Whitham [1955], Ponce et Simons [1977]. La dérivation rigoureuse de cette équation à partir des équations de Navier-Stokes est présentée.

L’équation de l’onde diffusante 1D classique

Dans cette section, l’équation de l’onde diffusante telle que classiquement utilisée en hydraulique fluviale est présentée, voir e.g. Lighthill et Whitham [1955], Ponce et Simons [1977].
Cette équation est obtenue en dérivant une relation algébrique Q(H, ∂xH) qui est ensuite injectée dans l’équation de conservation de la masse intégrée sur la section en travers (1.16a) pour obtenir une équation scalaire. L’équation de l’onde diffusante classique repose sur une approximation des équations de Navier-Stokes (1.1) à l’ordre 0 en ϵ qui permet d’obtenir facilement une relation Q(H, ∂xH).
En plus des termes négligés à l’ordre 1 pour obtenir les équations de Saint-Venant (1.16), cette approximation à l’ordre 0 implique que les termes d’inertie sont négligés. De ce fait, l’équation de l’onde diffusante est souvent présentée comme étant une approximation non-inertielle des équations de Saint-Venant.
Cette équation est très largement utilisée en pratique pour modéliser des écoulements 1D (voir e.g. Weill et al. [2014], chapitre 3 et les références citées), des écoulements 2D (voir e.g. Hromadka et al. [1985], Santillana et Daw-son [2010]) ou même des écoulements couplant 1D et 2D (voir e.g. [Aricò et al., 2016]).
D’autres approximations sont couramment utilisées. Celles-ci sont obtenues en négligeant un certain nombre de termes des équations de Navier-Stokes en fonction du régime de l’écoulement considéré. Le lecteur peut se référer
à Yen et Tsai [2001] et au chapitre 5 de Thual [2010] pour une revue des approximations classiques et à l’équation (55) Boutounet et al. [2016] pour un modèle à une équation multi-régime laminaire. L’équation de l’onde diffusante a l’avantage, par rapport aux équations de Saint-Venant et aux autres approxi-mations, d’être un bon compromis entre la simplification de l’équation des moments (1.14) et une modélisation relativement complexe et riche.
En effet, une relation algébrique relativement simple (1.20) est obtenue par l’approximation d’ordre 0 des équations de Navier-Stokes. Comme mentionné précédemment, cette relation algébrique permet d’obtenir une équation sca-laire qui à l’avantage d’avoir une complexité computationnelle inférieure au système de Saint-Venant.
D’un autre coté, cette équation permet de modéliser une physique relativement riche, notamment les effets de re-mous hydraulique, voir e.g. Ponce et Simons [1977], Yen et Tsai [2001], Thual [2010].
L’équation de l’onde diffusante a plusieurs autres avantages par rapport au système de Saint-Venant qui justi-fient son utilisation.
Dans le cadre de la modélisation d’écoulement adaptée à l’altimétrie, les conditions aux bords nécessaires sont des avantages. Comme mentionné précédemment, la résolution du système de Saint-Venant requiert d’imposer Qin en amont. Dans notre cadre de travail, imposer Qin en n’ayant accès qu’à des données altimétriques est un enjeu de taille. L’équation de l’onde diffusante, quant à elle, nécessite d’imposer Hu et Hd resp. en amont et en aval. Ces hauteurs sont directement observées par les satellites d’altimétrie et à cet égard, l’équation de l’onde diffusante est avantageuse par rapport au système de Saint-Venant.
Dans le chapitre 3, cette équation est étudiée et enrichie pour les écoulements à l’échelle des observations spatiales.
La dérivation rigoureuse de l’équation de l’onde diffusante classique à partir des équations de Navier-Stokes est présentée dans cette section. Cette équation est obtenue en approximant les équations de Navier-Stokes à l’ordre 0 du ratio géométrique ϵ, ce qui permet d’obtenir une relation algébrique Q(H, ∂xH). Les étapes d’intégration sur l’aire mouillée sont identiques aux étapes d’intégration pour la dérivation des équations de Saint-Venant.
Puis, des résultats sur l’étude théorique et numérique de l’équation de l’onde diffusante issus de la littérature sont présentés.

Etat de l’art de l’analyse mathématique de cette équation

Sous l’hypothèse d’une rivière très large et d’un écoulement graduellement varié, l’équation (1.23) peut aussi s’écrire sous la forme d’une équation de type chaleur non-linéaire : ∂ H − ∂ K (H − zb)γ ∂ Hs |∂xH|1−α t x x =a(H,∂xH) = 0 (1.26) avec γ = 53 et α = 12 .
Un terme source f(x, t) est classiquement rajouté dans la littérature en supposant f ≥ 0. Dans le cadre de ces travaux et pour être en accord avec la dérivation présentée précédemment, ce terme source est supposé nul.
Cette forme de l’équation est celle utilisée pour étudier les propriétés mathématiques de l’équation de l’onde dif-fusante. À noter que l’équation l’onde diffusante en 2D s’écrit aussi de manière naturelle sous cette forme. De plus, écrite dans cette forme plus générale, l’équation de l’onde diffusante permet aussi d’étudier d’autres équations non-linéaires, tel que l’équation des milieux poreux (zb = 0 et γ = 1) et l’équation du p-laplacien avec 1 < p < 2 (α = 0 et p = γ + 1), voir e.g. Santillana [2008] et les références citées.
L’équation de l’onde diffusante est une équation parabolique dite « doublement non linéaire » à cause du numérateur et du dénominateur du coefficient de diffusion a qui dépendent respectivement de H et de ∂xH. Les non-linéarités impliquent que cette équation est dégénérée quand H = zb et singulière quand ∂xH tend vers 0.
La nature doublement non-linéaire, dégénérée et singulière de l’équation fait de son analyse et de son étude un sujet compliqué. On peut notamment citer les travaux de J.-L. Lions (fin du XXe siècle) sur l’étude d’équations non-linéaires dégénérées, voir e.g. Lions [1969], bien que ce sujet de recherche est encore d’actualité, voir e.g. Alonso et al. [2008], Bögelein et al. [2021].
Du fait de la complexité de l’équation de l’onde diffusante dans sa forme générale, avec le terme source, les études de cette équation se font essentiellement au travers de sa forme faible : ∀ϕ ∈ W01,1+α(Ω) ∂tHϕ dx + Ks (H − zb)γ ∂xH∂xϕ dx = f ϕ dx|∂xH|1−α (1.27).
De plus, de nombreuses propriétés ont été démontrées uniquement dans le cas zb = 0. Bien que l’existence de solu-tions faibles a été montré dans un cadre général (zb ≠ 0) très récemment, l’unicité de solution faible, par exemple, n’est démontrée que dans le cas zb = 0. Pour une revue plus exhaustive des propriétés de cette équation dans le cas zb = 0, le lecteur peut se référer aux travaux de thèse Santillana [2008].
On rappelle que l’espace de fonctions Lp(X, Y ), appelé espace de Lebesgue, avec 1 ≤ p < +∞, est l’espace des fonctions dont la puissance d’exposant p est intégrable sur l’ensemble X et à valeurs dans Y : Lp(X, Y ) = {f | f(x) ∈ Y ∀x ∈ Y et X f(x)pdx < +∞}. Le cas p = +∞ correspond à l’espace des fonctions bornées sur X et à valeurs dans Y . X f(x)pdx 1/p. Lorsque p = 2, on définit aussi le produit.
Cet espace de fonctions est muni de la norme ∥f∥Lp(X) = scalaire associé f, g L2(X) = X f(x)g(x)dx.
L’espace de Sobolev W m,p(X, Y ) correspond à l’espace des fonctions dont toutes les dérivées jusqu’à l’ordre m sont dans Lp(X, Y ). De plus, l’espace W0m,p(X, Y ) correspond à l’espace des fonctions dans W m,p(X, Y ) et à support compact dans X.
A noter que quand l’ensemble Y n’est pas précisé, on prend pas défaut Y = R.

Problèmes inverses et assimilation de données

Cette section vise à présenter les problèmes inverses abordés dans ces travaux de thèse.
Dans un premier temps, une définition de problèmes inverses pour la modélisation physique est donnée puis déclinée pour les problèmes d’assimilation de données. Puis, l’approche variationnelle de l’assimilation de donnée, appelée VDA dans les autres chapitres, qui est utilisée dans ces travaux, est présentée plus en détail.
Ensuite, l’approche stochastique est rapidement abordée. Bien que cette dernière ne soit pas utilisée dans ces tra-vaux, cela permet de comprendre le choix de l’approche variationnelle et les liens qu’il peut y avoir entre celles-ci. Les problématiques de la covariance de l’erreur d’ébauche, point crucial de l’assimilation de données aussi bien pour l’approche variationnelle que stochastique, sont aussi présentées dans cette section.
Par ailleurs, une méthode d’identification parcimonieuse de termes de dynamique d’un modèle au sein d’un diction-naire et à partir de données, qui s’apparente à un problème inverse, est introduit à la fin de cette section.

Des problèmes inverses et de l’assimilation de données
Problèmes directs et problèmes inverses

De manière générale, un problème est dit l’inverse d’un autre problème lorsque les paramètres ou conditions nécessaires à la résolution du problème sont au moins partiellement la solution de cet autre problème, et inverse-ment. Il peut être alors souligné que le choix de quel problème est direct et quel problème es inverse peut être assez arbitraire.
La modélisation d’un système physique peut se formaliser par le problème suivant : connaissant les équations de la physique modélisant ce système, les paramètres du modèle ainsi que des conditions initiales et aux bords, trouver les variables d’état qui vérifient ces équations. Ce modèle et ce problème sont donc naturellement le modèle et le problème directs.
Cependant, en pratique, une difficulté majeure rentre en jeu : certains paramètres (dans un sens large, paramètres du modèle ou conditions) nécessaires pour résoudre le problème direct ne sont pas mesurés avec une précision et/ou une densité spatio-temporelle suffisantes, impliquant une prédiction des variables d’état peu ou pas assez précise. D’un autre côté, les techniques de mesures permettent souvent de mesurer plus facilement une grandeur calculable à partir des variables d’état du système.
De ce fait, dans le contexte des systèmes physiques et de leurs observations, on définit ainsi les problèmes inverses : connaissant des observations d’une grandeur calculable à partir des variables d’état du modèle direct ainsi que cer-tains paramètres du modèle direct, trouver les paramètres méconnus qui permettent au modèle direct de reproduire les états observés.
En mécanique des fluides, les modèles d’écoulements visent généralement à prédire la masse ainsi que le moment du fluide.
Dans le cas des équations de Saint-Venant 1D (1.16), cela se traduit par la prédiction des variables d’état (A, Q). Cependant, dans le cas d’observations spatiales, la bathymétrie et le coefficient de Strickler sont difficilement me-surables tandis que la hauteur de la surface libre H est facilement observable grâce à l’altimétrie et peut aisément être calculée à partir de A.
La bathymétrie zb et le coefficient de Strickler Ks seront donc nos paramètres méconnus du problème direct que l’on cherche à obtenir grâce à un problème inverse.
L’idée de trouver les causes d’un phénomène en observant les conséquences a de tous temps occupée les scien-tifiques dans différents domaines. Bien que de nombreux scientifiques se sont intéressés à des problèmes inverses spécifiques, les travaux de F. Gauss et de A.-M. Legendre au début du XIXe siècle ont posé la base de la méthode des moindres carrés et de beaucoup de problèmes inverses étudiés de nos jours.
Le lecteur peut se référer à Tarantola [2005] ou encore Kirsch [2011] pour plus de détails sur la théorie mathé-matique des problèmes inverses et des exemples issus de différents domaines de la science.

Sur l’existence et l’unicité de solution du problème d’optimisation

Bien qu’un terme de régularisation est ajouté pour espérer avoir un problème d’optimisation bien posé, l’existence et l’unicité de la solution sont rarement garanties.
Supposons que le système d’équations régissant le modèle direct est linéaire et coercive. On considère la fonction coût définie par l’expression (1.29) avec les termes (1.30) et (1.31), i.e. la fonction coût est linéaire quadratique, et Kad est un ensemble convexe fermé. Alors, la fonction coût est strictement convexe et le problème de minimisation (1.28) admet un unique minimiseur. La démonstration, classique en théorie du contrôle optimal, peut être trouvée e.g. dans Lions [1971]. En pratique, le système d’équations régissant le modèle direct n’est évidemment pas linéaire, voir par exemple les équations de Saint-Venant (1.16) ou l’équation de l’onde diffusante (1.25).
Dans ce cas de figure, l’existence et l’unicité du minimiseur ne sont pas garanties. Bien que l’on suppose l’existence de minimiseurs sans le démontrer, la fonction coût n’est très probablement pas convexe et il peut y avoir plusieurs minima locaux, voir e.g. Bocquet [2014], Monnier [2018]. Le terme de régularisation permet de “convexifier” la fonction coût. Cependant, il est compliqué de savoir à partir de quel moment le terme de régularisation a “assez convexifié”, i.e la fonction coût est convexe dans un voisinage du minimum global qui contient kb, et même si le minimum global est proche de kt, ce qui dépend de la pertinence du terme de régularisation.
De plus, du fait de la nature des écoulements considérés dans les présents travaux et de leur sensibilité aux contrôles, la fonction coût a tendance à être relativement plate et à varier peu quand le contrôle est significativement perturbé. Cela implique que la hessienne de j est mal conditionnée impliquant le mauvais conditionnement et donc le caractère mal posé du problème d’optimisation.

Équivalence entre les approches variationnelles et stochastiques

Comme mentionné précédemment, l’estimateur du maximum de log-vraisemblance de l’analyse (donné par l’ex-pression (1.35)) pour des erreurs gaussiennes (impliquant que la fonction de log-vraisemblance est donnée par l’expression (1.36)) est identique à la solution du problème variationnel (1.28) avec la fonction coût (1.29) définie par les termes (1.30) et (1.31).
On rappelle que le filtre de Kalman est exact et optimal lorsque les erreurs sont gaussiennes et l’opérateur d’observa-tion est linéaire. On peut conclure qu’il y a équivalence entre le filtre Kalman et l’algorithme 4D-Var au temps final lorsque le modèle direct est parfait (i.e. l’erreur de modélisation est nulle) pour un même problème d’assimilation de données (mêmes observations et ébauche initiale). Ainsi, l’analyse finale calculée par le filtre de Kalman et la valeur finale de la trajectoire optimale (prédiction effectuée à partie de l’analyse) calculée par l’algorithme 4D-Var sont égales dans ce contexte, voir e.g. Bouttier et Courtier [2002], Bocquet [2014].

Avantages et inconvénients des deux approches

Le filtre de Kalman étendue se base sur la linéarisation (1.37) de l’opérateur d’observation non-linéaires. Cependant, cela suppose que l’opérateur d’observation est linéaire dans le voisinage de la valeur d’ébauche du contrôle. En pratique, il est alors nécessaire que les non-linéarités sont « relativement faibles », i.e. les phénomènes physiques impliquant les non-linéarités dans les équations ont un impact relativement limité sur l’écoulement mo-délisé.
Dès lors que ces non-linéarités sont fortes, le filtre de Kalman étendu peut diverger, voir plus de détails sur cette hypothèse dans Bouttier et Courtier [2002] et un exemple de filtre divergent dans Bocquet [2014].
Le filtre de Kalman d’ensemble a été introduit dans le but de mieux prendre en compte ces non-linéarités.
Par ailleur, dans l’approche variationnelle, les non-linéarités sont naturellement prises en compte et sans avoir besoin d’une approximation. Ainsi, dans notre cas d’inférence de zb et/ou Ks dans les modèles d’écoulement considérés ici, l’approche variationnelle est bien adaptée du fait d’opérateurs d’observation non-linéaires.
Le filtre de Kalman et ses variantes reposent sur la probabilité conditionnelle des différentes erreurs qui peuvent être étudiées comme des processus aléatoires, voir e.g. Lorenc [1986].
Cependant, cela nécessite des connaissances sur les propriétés statistiques de ces erreurs. Cela est surtout vrai pour le filtre de Kalman d’ensemble où la perturbation de la valeur d’ébauche du contrôle doit suivre la densité de pro-babilité de l’erreur d’ébauche, voir Evensen [1994].
Dans notre contexte applicatif, on rappelle que le contrôle est zb et/ou Ks. En pratique, celui-ci est soit très mal mesuré, soit mesuré de manière indirecte et dépendante des données, soit pas mesuré du tout, voir section 1.1. Cela implique que les propriétés statistiques de l’erreur d’ébauche sont peu ou pas connues. Cette méconnaissance de l’erreur d’ébauche et de ses statistiques est aussi une raison qui pousse à utiliser le terme de régularisation (1.33) basé sur le gradient du contrôle plutôt que le terme d’écart à la valeur d’ébauche (1.31) dans l’approche variation-nelle. Ainsi, lorsque les propriétés statistiques des erreurs sont mal connues, l’approche stochastique est plus difficile à mettre en place que l’approche variationnelle qui semble être plus adaptable.
Dans le filtre de Kalman, il est possible de prendre en compte l’erreur du modèle direct, notamment pour améliorer la covariance de l’erreur d’ébauche du cycle suivant. À l’inverse, dans l’approche variationnelle, il est supposé que le modèle est parfait ou que les erreurs de celui-ci sont négligeables, voir e.g. Carrassi et al. [2018]. Dans le cas de ces travaux, les erreurs de modélisation sont multiples et peu connues. On peut notamment citer les erreurs relatives aux conditions aux bords ou les erreurs dues aux hypothèses de modélisation telles que l’hypothèse d’un écoulement 1D ou les hypothèses sur la forme des sections en travers. Ainsi, du fait de ces erreurs, le contrôle optimal sert de contrôle équivalent qui permet au modèle 1D de compenser les erreurs de modélisation. Ce contrôle équivalent peut être assez éloigné de kt mais permet d’obtenir un modèle 1D cohérent avec les observations.
Des discussions détaillées sur les avantages et inconvénients de chaque approche peuvent être trouvées dans la lit-térature, voir e.g. Bouttier et Courtier [2002], Bocquet [2014], Carrassi et al. [2018].
Dans notre contexte d’observations des écoulements fluviaux par les satellites, du fait des non-linéarités des modèles d’écoulement et de la méconnaissance de l’erreur d’ébauche, l’approche variationnelle nous semble plus adaptée que l’approche stochastique. Cela explique le choix de la méthode variationnelle dans le contexte de ces travaux de thèse. L’assimilation variationnelle permet d’obtenir un contrôle équivalent et optimal. Ainsi, le modèle d’écoulement 1D associé et la prédiction du débit qui en découle, sont cohérents avec les mesures altimétriques de la hauteur de la surface libre.

Sur la covariance de l’erreur d’ébauche en assimilation de données

En assimilation de données, le terme de régularisation (1.31) et le changement de variable (1.32) mettent en avant l’opérateur de covariance de l’erreur d’ébauche C.
L’estimation de cet opérateur peut avoir un impact important sur la qualité du résultat de l’assimilation, notam-ment en terme de précision et en terme de vitesse de convergence, voir e.g. Haben [2011].
Il est mis en avant comme étant un préconditionnement de la hessienne de la fonction coût dans Haben et al. [2011]. De plus, sous les hypothèses menant à l’analyse BLUE, la fonction coût (1.29) définie par les termes (1.30) et (1.31) vaut : ∇2j(k) = 2 C−1 + H∗R−1H . Ainsi, le caractère convexe de la fonction coût j dépend fortement de l’opérateur C, voir e.g. Bouttier et Courtier [2002], Haben [2011] pour plus de détail sur la hessienne et figure 1.10.
Il s’agit donc d’un sujet crucial mais aussi complexe, voir une revue sur la question dans Bannister [2008a,b]. Deux types de méthodes pour estimer cet opérateur de covariance sont principalement utilisées et sont rapidement présentées ici.
Le lecteur peut se référer à la revue faite dans Mirouze [2010] qui listent de manière assez complètes les différentes méthodes pour estimer cet opérateur ou même son inverse.
Dans le cadre d’un problème d’assimilation multi-varié (plusieurs variables de contrôle dans le vecteur de contrôle), l’opérateur de covariance ne contient pas seulement la covariance associée à une variable de contrôle en plusieurs points de l’espace (covariance univariée) mais aussi la covariance entre les variables de contrôles (covariance croisée). Par exemple, dans un cadre discret, la matrice de covariance contient les matrices de covariance univariée dans les blocs sur la diagonale et les matrices de covariance croisée dans les autres blocs.
Il est couramment supposé que les variables sont décorrélées entre elles. Les covariances croisées sont alors nulles et la matrice de covariance est diagonale par blocs. C’est notamment le cas dans ces travaux de thèse.
Une possibilité pour prendre en compte la corrélation entre les variables est de trouver un changement de variable qui permet d’obtenir des variables décorrélées, ou du moins pour lesquelles l’hypothèse de variables décorrélées est mieux respectée. Ensuite, le problème est traité comme un problème avec des variables de contrôle décorrélées, voir e.g. Derber et Bouttier [1999].

Table des matières

1 Contexte et état de l’art 
1.1 Programmation par Contraintes
1.1.1 Formalisme de la programmation par contraintes
1.1.2 Méthodes de recherche arborescente
1.1.3 Autres approches
1.2 Apprentissage par renforcement
1.2.1 Principes de l’apprentissage par renforcement
1.2.2 Algorithmes d’apprentissage par renforcement
1.2.3 Fonction d’approximation
1.2.4 Algorithme REINFORCE
1.2.5 Apprentissage par renforcement pour l’optimisation combinatoire
1.3 Recherche arborescente de Monte Carlo
1.3.1 Principes de la méthode MCTS
1.3.2 Description de l’algorithme
1.3.3 Algorithme de MCTS pour l’optimisation combinatoire
1.4 Apprentissage pour l’optimisation combinatoire
1.4.1 Apprendre à résoudre
1.4.2 Apprendre à chercher
1.4.3 Apprendre à configurer
2 Proposition d’un cadre générique pour la résolution de problèmes combinatoires 
2.1 Apprentissage par renforcement d’heuristiques
2.1.1 Processus de décision markovien pour la résolution de problème combinatoire
2.1.2 Politique de décision pour caractériser une heuristique de choix de valeurs
2.1.3 Algorithme d’apprentissage d’une heuristique de valeurs
2.1.4 Intégration de l’heuristique dans une recherche arborescente
2.2 Recherche arborescente de Monte Carlo
2.2.1 Utilisation des bornes
2.2.2 Recherche en profondeur
2.2.3 Compromis dynamique
2.3 Synthèse
3 Problème de tournées de chariots dans un atelier d’assemblage 
3.1 Description du problème
3.2 Travaux connexes
3.2.1 Liens avec des problèmes de la littérature
3.2.2 Modèle existant basé sur LocalSolver
3.3 Modèles de programmation par contraintes
3.3.1 Modèle d’ordonnancement
3.3.2 Modèle de voyageur de commerce
3.3.3 Stratégie de branchement
3.4 Évaluation expérimentale des modèles de programmation par contraintes
3.4.1 Jeux de données
3.4.2 Configuration
3.4.3 Résultats expérimentaux
3.5 Apprentissage par renforcement d’heuristiques de choix de valeurs
3.5.1 Processus de décision markovien
3.5.2 Caractérisation de l’heuristique de branchement
3.5.3 Intégration de l’heuristique apprise dans des méthodes arborescentes
3.5.4 Intégration de l’heuristique apprise dans une méthode de recherche locale
3.5.5 Résultats expérimentaux
3.6 Recherche arborescente de Monte Carlo
3.6.1 Algorithme MCTS pour le problème de tournées de chariots
3.6.2 Résultats expérimentaux
3.7 Synthèse
4 Problème de chargement de camions 
4.1 Description du problème
4.2 Travaux connexes
4.2.1 Liens avec des problèmes de la littérature
4.2.2 Algorithme existant dans l’entreprise
4.3 Proposition d’une méthode de recherche arborescente
4.3.1 Approche itérative
4.3.2 Stratégies de placement et d’exploration
4.3.3 Caractérisation de l’incomplétude
4.4 Apprentissage par renforcement de la stratégie de branchement
4.4.1 Processus de décision markovien
4.4.2 Caractérisation de l’heuristique de branchement
4.4.3 Résultats expérimentaux
4.5 Recherche arborescente de Monte Carlo
4.5.1 Algorithme MCTS pour le problème de chargement de camions
4.5.2 Résultats expérimentaux
4.6 Synthèse
Conclusion et perspectives 
Bibliographie 

Télécharger le rapport complet