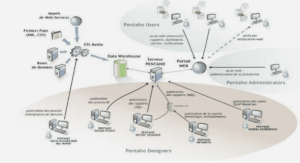
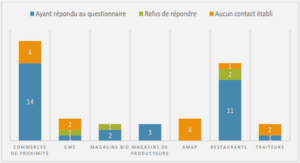
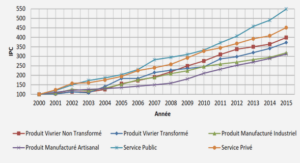
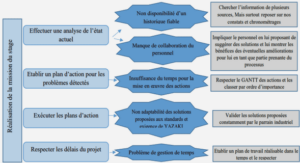
The dissimilarity representation (DR) provides a classification space that is defined by some proximity measure. One case where the DR approach is advantageous is when patterns are represented in high-dimensional feature spaces, and only simple classification rules are applicable. For instance, bio-cryptographic schemes use biometric signals to secure cryptographic keys. These schemes mostly employ an error correction code that is considered as a simple threshold classifier. In addition, for behavioral biometrics, e.g., handwritten signatures, effective verification systems rely on high-dimensional feature representations and complex classifiers. It is a challenge to produce discriminant bio-cryptographic implementations based on behavioral biometrics, with these limitations on representation size and classification complexity. In this chapter, an approach is proposed for optimization of DRs, so that a concise representation is discriminant even by employing a simple threshold classifier. To this end, high-dimensional feature representations are translated to an intermediate space, where pairwise feature distances are the space constituents. Then, Boosting Feature Selection algorithm is applied in this intermediate space, and produces an adaptive dissimilarity measure that relies on a concise feature representation. This measure generates the final dissimilarity space, where pattern proximities to some prototypes are the space constituents. Finally, discriminant prototypes are selected in the dissimilarity space for enhanced representation. The proposed approach is applied to classical and bio-cryptographic systems for offline signature verification. Proof of concept simulations on the Brazilian signature database indicate the viability of the proposed approach. Concise DRs with only 20 features and a single prototype are produced. With employing a simple threshold classifier, the produced DRs have shown state-of-the-art accuracy of about 7% average error rate, as that of complex systems in the literature. The content of this chapter was published at the 2nd International workshop on Similarity-Based Pattern Analysis and Recognition (Eskander et al., 2013f), the 2nd International workshop on Automated Forensic Handwriting Analysis (Eskander et al., 2013a), and submitted to the special issue of the IEEE Transactions on Neural Networks and Learning Systems on « Learning in non-(geo)metric spaces » (Eskander et al., 2013e).
From learning features to the dissimilarity representation
Designing a classifier relies somewhat on the concept of dissimilarity. Ideally, similar objects should produce similar classification labels and dissimilar objects should produce dissimilar labels. Similarity learning takes place either implicitly or explicitly, based on the applied representation and learning strategy. In this section, we discuss these different forms and their relation to the proposed approach .
Learning feature representations
The approach to independently design a FR, as a pre-processing step for the classifier design, is known as filter feature selection approach (Guyon and Elisseeff, 2003). As the compactness and isolation of different class distributions implies that real dissimilarities between objects are captured, some methods rely on these measures to guide the feature selection process. For instance, the Fisher criterion is extensively employed, where the ratio between WC and BC variance reflects the effectiveness of the representation (Fisher, 1936). This approach, mostly, involves optimization problems that becomes infeasible, when large number of classes are represented by few training samples and high dimensional feature extractions.
Alternatively, some methods, namely, wrapper and embedded feature selection, combine the design of both representation and classifier in a single process. For the wrapper approach, a fixed predictor is tested based on different candidate representations, where the minimum classification error determines the best representation (Kohavi and John, 1997). For the embedded approach, the predictor is built and tuned concurrently with selection of an effective representation. Examples under this category are classification and regression trees (CART) (Breiman et al., 1984), and boosted feature selection (BFS) (Tieu and Viola, 2004), where individual features are selected in a greedy manner, while building the classifier. Although they make searching in high dimensional spaces more tractable, these methods do not produce generic representations, as they tune the representation to specific classification rules. Moreover, feature selection techniques do not necessarily produce FRs that generalize for unseen classes and samples during operations.
Learning distance functions
A more explicit way for dissimilarity learning is done with classifiers that take explicit distances (or kernels) as inputs, e.g., KNN, SVM, etc. For such distance/kernel-based classifiers, a distance function that measures the true proximity between FRs of patterns are firstly designed, then they are fed to the classification stage. Performance of such classifiers relies on the quality of the resulting proximity measure, which in turn relies on the employed FR, the distance function applied to the representation, and the prototypes that used as references for distance computations.
Learning dissimilarity representations
Recently, the concept of distance function learning is generalized to learning dissimilarity representations (DRs) (Pekalska and Duin, 2002). While distance functions are restricted to be feature-based and metric, conversely, these conditions are relaxed in the DRs, so any proximity measure can be employed. Through this, the statistical pattern recognition methods are applicable to subjects indescribable by traditional feature representation and/or that involve none metric proximities. Previously, such subjects could only be classified through structural pattern recognition methods, hence, the DR approach is considered as a bridge between structural and statistical pattern recognition techniques. In addition, the DR approach can also be applied to feature-based systems, where the learning and classification tasks are more tractable in the DR space than in the FR space. This last scenario relies on same reasoning like that of the kernel trick, while, here, any proximity measure can be employed (Pekalska and Duin, 2005).
|
Table des matières
INTRODUCTION
CHAPTER 1 BACKGROUND
1.1 Biometric systems
1.1.1 Performance of biometric systems
1.1.2 Handwritten signature biometrics
1.2 Bio-cryptography
1.2.1 Bio-cryptographic schemes
1.2.2 Fuzzy Vault scheme .
1.2.2.1 State of the art of FV
CHAPTER 2 OPTIMIZED DISSIMILARITY REPRESENTATIONS
2.1 Introduction
2.2 From learning features to the dissimilarity representation
2.2.1 Learning feature representations
2.2.2 Learning distance functions
2.2.3 Learning dissimilarity representations
2.2.4 Proposed approach
2.3 Dissimilarity Representation Optimization approach
2.3.1 Feature selection and dissimilarity learning
2.3.2 A two-step feature selection approach
2.3.3 Adaptive dissimilarity measure
2.3.4 Prototype selection in the dissimilarity space
2.4 Application to signature verification
2.4.1 Dissimilarity-based signature verification
2.4.2 Applying the proposed approach
2.5 Application to bio-cryptography
2.5.1 Dissimilarity-based bio-cryptography
2.5.2 Applying the proposed approach
2.6 Experiments
2.6.1 Database
2.6.2 Class-independent optimization
2.6.2.1 Feature extraction
2.6.2.2 Class-independent feature selection
2.6.3 Class-specific optimization
2.6.3.1 Class-specific feature selection
2.6.3.2 Prototype selection in the D-space
2.6.4 Performance evaluation
2.6.5 Results and discussion
2.7 Conclusion
2.8 Discussion
CHAPTER 3 A HYBRID OFFLINE SIGNATURE VERIFICATION SYSTEM
3.1 Introduction
3.2 Pure WD and WI signature verification systems
3.3 A Hybrid WI-WD signature verification system
3.3.1 Theoretical basis
3.3.2 System overview
3.3.3 WI training
3.3.4 WD training
3.3.5 Signature verification .
3.3.5.1 WI-SV mode
3.3.5.2 WD-SV mode
3.4 Experimental methodology
3.4.1 Signature databases
3.4.1.1 Brazilian database
3.4.1.2 GPDS database
3.4.2 Feature extraction
3.4.3 WI training
3.4.4 WD training
3.4.5 Performance measures
3.5 Simulation results
3.5.1 Performance of the WI and WD verification modes
3.5.1.1 Brazilian database
3.5.1.2 GPDS database
3.5.1.3 Computational complexity
3.5.2 Comparisons with systems in the literature
3.5.2.1 Brazilian database
3.5.2.2 GPDS database
3.6 Conclusions and future work
3.7 Discussion
CHAPTER 4 A BIOMETRIC CRYPTOSYSTEM BASED ON SIGNATURES
4.1 Introduction
4.2 Fuzzy Vaults with offline signatures
4.2.1 Fuzzy Vault
4.2.1.1 FV encoding
4.2.1.2 FV decoding
4.2.2 Encoding Fuzzy Vaults with signature images
4.3 Selection of a user-specific signature representation
4.3.1 Feature selection in the feature dissimilarity space
4.3.2 A two-step BFS technique with dissimilarity representation
4.3.2.1 Population-based feature selection
4.3.2.2 User-based feature selection
4.4 A Fuzzy Vault system for offline signatures
4.4.1 Enrollment process
4.4.2 Authentication process
4.4.3 Security analysis
4.5 Experimental results
4.5.1 Experimental methodology
4.5.1.1 Database
4.5.1.2 Feature extraction
4.5.1.3 Feature selection
4.5.1.4 FV parameter values
4.5.1.5 Performance measures
4.5.2 Results on quality of feature representation
4.5.3 Results on performance of the FV system
4.5.4 Computational complexity
4.6 Conclusions and future work
4.7 Discussion
GENERAL CONCLUSION
![]() Télécharger le rapport complet
Télécharger le rapport complet