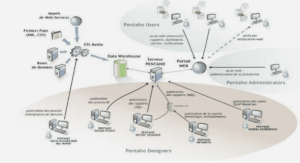
Network of distributed data centers (NDC) with cloud capabilities refers to several data centers which are positioned in geographically diverse locations and support compatible virtualization technologies. These data centers are well connected, and live VM migration is possible among them. Generally, a global scheduler is responsible to dispatch and manage the applications on these data centers. The type of this scheduler usually defines the type of the NDC. Therefore, the operation of an NDC can be imagined as a job scheduling problem. However, scheduling of jobs on computing resources cannot be always expressed as a single and unique problem statement. This is mainly because of high level of diversity in the possible compute configurations and also types, structures, and goals of computing jobs. That means that there is a spectrum of concepts that we may encounter when analyzing a specific configuration. In (Xhafa and Abraham, 2010), some of those concepts are described and discussed, and we just list them to show some of complexity of subject matter: heterogeneity of resource, heterogeneity of jobs, local schedulers, meta-scheduler, batch mode scheduling, resource-oriented schedulers, application oriented schedulers, heuristic and metaheuristic methods for scheduling, local policies for resource sharing, job-resource requirements, and security. In particular, schedulers can be divided in three main categories: i) Local/Host Schedulers: The scheduler has the complete picture of its resources (free time slots, etc). In the case of super scheduler, see below, local schedulers also exist but they only follow the reserved slots determined by the super scheduler, ii) Meta Schedulers (Brokers): A meta scheduler distributes incoming jobs among a few local schedulers. Therefore, meta scheduler does not determine of the actual time slot assigned to a job. Instead, it uses the statistics of free resources reported by local schedulers to distribute the jobs, and iii) Super Schedulers: A super scheduler merges both local and meta scheduling strategies. Local schedulers first report actual free time slots to the super scheduler, and it then assigns jobs to them. This is the most efficient scheduler. However, it requires constant communication between schedulers, and solving the assignment problem could be very time consuming and ineffective especially in the case of high number of resources. In the following sections, several actual schedulers with goal functions toward performance, energy, carbon, profit, and QoS targets are presented.
Performance-Aware Scheduler
Scheduling of jobs on a distributed computing system, such as a network of data centers, is an old and well studied problem. For example, in Braun et al. (2001), several heuristic scheduling algorithms based on the makespan matrix, such as Opportunistic Load Balancing (OLB) and Minimum Completion Time (MCT), were introduced. It is worth noting that these algorithms consider assignment of jobs to machines, not to the processors. Therefore, their approach should be considered as a global scheduler. A global scheduler is not necessarily always a distributed scheduler. For example, a scheduler that works within a data center can work in a global manner, while it obviously is not a distributed scheduler. They also considered GA as one of their schedulers. For simulations, Expected Time to Compute (ETC) matrix were used. Also, proper synthesizd ETC matrices were used in order to simulate a heterogeneous computing environment.
Another milestone in the scheduling of computing resources is Freund et al. (1998), which introduced MaxMin and MinMin heuristic schedulers. Similar to Braun et al. (2001), only performance in terms of completion time was considered, and there was no account for the energy consumption or carbon footprint of the operations. They performed their calculations using a simulated environment, called SmartNet.
In Maheswaran et al. (1999), the k-Percent Best (KBP) and Switching Algorithm (SA) schedulers were introduced along with the Minimum Execution Time (MET), Minimum Completion Time (MCT), Suffrage, and Opportunistic Load Balancing (OLB) heuristic schedulers. The kpercent best (KPB) scheduler considers only a subset of machines while mapping a job. The subset is formed by picking the (k/100)m best machines based on their execution time of that job, where 100/m≤k≤100 and m is the number of machines. The job is assigned to a machine that provides the earliest completion time in the subset. The main idea behind KBP is not to map a job on the best machine, but it is to avoid mapping a job on a machine that could be a better choice for a yet-to-arrive job. If k = 100, then the KPB heuristic is actually reduced to the MCT heuristic. For the case k = 100/m, the KPB heuristic is equivalent to the MET heuristic.
The SA scheduler uses the MCT and MET schedulers in a cyclic fashion depending on the load distribution across the machines. In this way, the SA tries to make benefit of the desirable properties of both MCT and MET. The MET heuristic can potentially create load imbalance across machines by assigning many more jobs to some machines than to others, whereas the MCT heuristic tries to balance the load by assigning jobs for earliest completion time. If the jobs are arriving in a random mix, it is possible to use the MET at the expense of load balance until it reaches a given threshold, and then use the MCT to smooth the load across the machines.
In Kim et al. (2003), in addition to MaxMin and MaxMax algorithms, the Percent Best scheduler was considered. The Percent best scheduler, which is a variation of the aforementioned k-Percent Best scheduler (KBP) (Maheswaran et al., 1999), tries to map jobs onto the machine with the minimum execution time while considering the completion times on the machines. The idea behind this scheduler is to pick the top m machines with the best execution time for a job, so that the job can be mapped onto one of its best execution time machines. However, limiting the number of machines to which a job can be mapped, may cause the system to become unbalanced. Therefore, the completion times are also considered in selecting the machine to map the job. The scheduler clusters the jobs based on their priority. Then, starting from the high priority group, for every job in this group, it finds the top m(=3) machines that give the best execution time for that job. Then, For each job, it finds the minimum completion time machine from the intersection of the m-machine list and the machines that are idle. For jobs with no tie, the mapping is performed immediately. For those jobs that are in a tie with some other jobs, that job that has earliest primary deadline is mapped first. The process is continued until all jobs in the high priority group are mapped. Then, the same procedure is applied to the jobs of other lower priority groups. They considered an increase in m when the priority of group decreases. In addition to the Percent Best scheduler, they introduced the Queuing Table, the Relative Cost, the Slack Suffrage, the Switching Algorithm, and the Tight Upper Bound (TUB) schedulers. The Queuing Table scheduler, which considers urgency in its mapping process, uses the Relative Speed of Execution (RSE), which is the ratio of the average execution time of a job across all machines to the overall average job execution time for all tasks across all machines, and a threshold to divide jobs into two categories of fast and slow. Using this categorization, and also estimating the nearness of the jobs deadline, the scheduler first maps those jobs that are in higher “urgency”. The Slack Suffrage scheduler, which is a variation of the Suffrage scheduler Maheswaran et al. (1999), uses a positive measure of percentage slack of all jobs on all machines with various deadline percentages, and then maps those jobs with tighter deadline (higher deadline factor that was estimated for that job when enforcing positivity of the percentage slack measure). Please note that the Relative Cost scheduler does not have any direct relation with profit, and in fact the cost was defined based on the completion time. Cases of high and low heterogeneity and also tight and loose deadlines were also considered. It was observed that the Max-Max works the best in the high heterogeneity and loose deadlines cases, while the Slack Suffrage heuristic was the best in the low heterogeneity and loose deadlines cases. In those cases with tight deadlines, all schedulers showed low performance. Relatively, in the highly heterogeneous and tight deadlines cases, Max-Max and Slack Suffrage were better, while Queueing Table performed better in the low heterogeneity and tight deadlines cases.
|
Table des matières
INTRODUCTION
0.1 Context
0.2 Problem Statement
0.3 Objectives
0.4 Thesis Outline
CHAPTER 1 LITERATURE REVIEW
1.1 Network of Distributed Data Centers with Cloud Capabilities
1.1.1 Performance-Aware Scheduler
1.1.2 Energy-Aware Scheduler
1.1.3 Profit-Aware Scheduler
1.1.4 Other type of Schedulers
1.2 Server Consolidation and Load Balancing in Cloud Computing
1.2.1 Grouping Genetic Algorithm in Server Consolidation
1.2.2 Grouping Mechanism in Grouping Genetic Algorithm
1.3 Server Energy Metering
1.4 Cooling System Power Modeling
1.4.1 Computer room (CR)
1.4.2 Chillers
1.4.3 Cooling tower (CT)
1.4.4 Heat Handling Capacity in a Datacenter
1.5 Simulation Platforms for Energy Efficeiny and GhG Footprint in Cloud Computing
1.5.1 CloudSim
1.5.2 GreenCloud
1.5.3 iCanCloud
1.5.4 MDCSim
1.6 Chapter Summary
CHAPTER 2 CARBON-PROFIT-AWARE GEO-DISTRIBUTED CLOUD
2.1 State-of-the-Art Geo-DisC Architecture (Baseline Design)
2.1.1 Energy Model
2.1.2 Carbon Footprint and Pricing
2.1.3 Scheduler Features
2.1.4 HPC Workload Features
2.1.5 Summary
2.2 Carbon-Profit-Aware Geo-DisC Architecture (Our Proposed Design)
2.2.1 Component Modeling
2.2.2 Carbon-Profit-Aware Scheduler
2.2.3 MLGGA Load Balancer for Web Applications
2.2.4 Managers and Controllers
2.2.5 Summary
2.3 Chapter Summary
CHAPTER 3 GEOGRAPHICALLY DISTRIBUTED CLOUD MODELING
3.1 IT Equipment Modeling
3.1.1 Profit per Core-Hour-GHz
3.1.2 Power Metering Model for Servers
3.1.3 NDC Carbon-Related Metrics
3.2 Cooling System Modeling
3.2.1 The Temperature Altitude Aware Model (TAAM)
3.2.2 Set of Equations of the Cooling System Model
3.2.3 Summary
3.3 Chapter Summary
CHAPTER 4 CARBON-PROFIT-AWARE JOB SCHEDULER
4.1 Scheduling Metrics
4.1.1 Energy and Carbon
4.1.2 Carbon Tax
4.1.3 Profit per Core-Hour-GHz
4.1.4 Summary
4.2 Optimization Problem
4.3 CPA Scheduler Algorithm
4.3.1 Optimum Frequency Calculation
4.3.2 Virtual Carbon Tax
4.3.3 Summary
4.4 Expected Outcome
4.4.1 Performance
4.4.2 Virtual Carbon Tax
4.5 Chapter Summary
CHAPTER 5 CARBON-AWARE LOAD BALANCER
5.1 Multi-Level Grouping Genetic Algorithm
5.1.1 MLGGA Crossover
5.1.2 MLGGA Mutation
5.1.3 Extensions of the MLGGA Crossover and Mutation
5.2 Carbon-Aware Load Balancing Concept
5.3 Chapter Summary
CHAPTER 6 EXPERIMENTAL RESULTS AND VALIDATION
6.1 Simulation Environment
6.1.1 Batch Simulation
6.1.2 Caching
6.1.3 Summary
6.2 Green HPC Job Scheduling Scenarios
6.2.1 Experimental Setup
6.2.1.1 Comparing Algorithms
6.2.2 CPA Scheduler Performance Study
6.2.3 Seasonal Energy-Variations Study
6.2.4 Cooling System Study
6.2.5 Virtual Carbon Tax Study
6.2.5.1 Carbon-Profit Trade-Off in CPAS with VCT
6.2.5.2 Study of CPA Scheduler based on Virtual GHG-INT Equivalent Carbon Tax
6.2.6 Summary
6.3 Server Power Metering Validation
6.3.1 Experimental Setup
6.3.1.1 Server Power Metering Setup ..
6.3.1.2 VM migration Power Metering Setup
6.3.2 Server Power Metering Validation Results
6.3.3 VM Migration Power Metering Validation Results
6.4 Low-Carbon Web Application Load Balancing
6.4.1 Experimental Setup
6.4.1.1 Optimization Problem
6.4.2 MLGGA Performance Analysis on Large Scale CADCloud
6.4.2.1 MLGGA Comparison Results
6.4.3 Energy Diversity Study
6.4.3.1 Results
6.4.4 MLGGA Performance Study on Real Data
6.4.5 MLGGA Convergence Time
CONCLUSION
![]() Télécharger le rapport complet
Télécharger le rapport complet