Multi-hypothesis sequential ratio test guided by list decoding

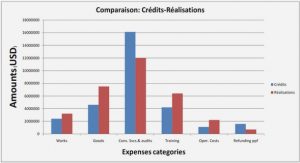
OFDM transmission scheme

Multicarrier communications are used to achieve high data transmissions while is maintained a negligible inter-symbol interference (ISI). There are different ways of implementing multicarrier communications such as frequency division multiplexing (FDM), discrete multi-tone (DMT) and orthogonal frequency division multiplexing (OFDM). In OFDM, the information is transmitted in parallel form over L different subchannels centered at different orthogonal subcarrier frequencies. The orthogonal subcarrier signals are overlapped in frequency spectrum for improving the spectral efficiency and they are spaced by Δ f = 1/T to maintain the orthogonality during the symbol interval T. In other words, the total system bandwidth W is divided into L = W/Δ f subchannels of width Δ f. The bandwidth of each subchannel Δ f is chosen sufficiently small to ensure that each subchannel experience flat fading, so that ISI is mitigated on each subchannel. Furthermore, OFDM transmissions add a guard interval called cyclic prefix (CP) to each transmitted OFDM symbol in order to completely eliminate the ISI.

Sequential detection guided by error-detecting codes The second option for decreasing the average detection latency under sequential detections is employing error-detecting codes. In this sequential detection scheme, the error-detecting code acts as a ’genie’ that identifies if the detected message is correct or not at certain detection time τi. Sequential tests using error-detecting codes are executed until there is not error on data, namely as soon as the decoder has not found errors in the received message. An errordetecting code commonly used is the Cyclic-redundancy-check (CRC) code. Error-detecting CRC codes are likewise used as outer codes to improve the error correction performance of inner codes. For instance, when list decoders are employed by inner codes such as turbo codes or polar codes (Narayanan & Stuber (1998); Tal & Vardy (2015)), the CRC code is used to choose a valid path from the generated list. With the purpose to recover an erroneous message instead of to discard it, Wang et al. (2008) proposes an iterative CRC-assisted decoding of convolutional codes. A concern related with this CRC-based scheme is that too early detections produce a bad error performance over noisy channels. This issue will be managed in this project. Moreover, Au & Gagnon (2016) show that under an optimized CRC-based early detection scheme the average detection latency (τ¯) is decreased while the block-error probability is the same of synchronous detections. In this work, we will try to determine the best possible setting to obtain the mentioned results.

Selection of CRC polynomials

Considering that the size of the CRC or check sequence is equal to the degree of the generator polynomial (r = n − k) of an (n,k) CRC code, we refer to this code as CRC-r. The normal representation of a CRC polynomial is the binary or hexadecimal notation of its coefficients. For example the CRC-5/ITU uses the CRC polynomial X5 +X4 +X2 +1, which is represented by 110101 or 0x15 in binary or hexadecimal notation, respectively. Alternatively, the CRC polynomial representation can omit the coefficient of the term X0, since it is always 1. This representation is proposed by Koopman (2002). Hence, the polynomial of the example also can be denoted as 11010 or 0x1A. It is well known that different cyclic redundancy checks are employed in technical standards. For the same CRC size there are different CRC polynomials or generator polynomials G(X), Cook (2016). For instance, there are three, fourteen, and twenty-eight CRC polynomials reported for CRC-5, CRC-8 and CRC-12, respectively. Considering that there is a variety of published CRC polynomials, now the question is which polynomial do we choose? Koopman & Chakravarty (2004) describe how to select good CRC polynomials based on the desired Hamming distance, the data word length and the desired CRC size. They have found there are other CRC polynomials that provide a better error detection capacity. The performance of CRC polynomials is evaluated in terms of the probability of undetected errors (Pud) under an assumed random independent bit-error rate (BER).

The best achievable performance is the lowest bound computed by an exhaustive search of all polynomials for each data word length assuming a BER of 10−6 as shown in Figure 1.8. The CRC polynomial performance depends on its Hamming weight. Hamming weight (HW) is the number of undetectable errors for a given number of bit-errors, e.g. 1267 undetectable 2-bit errors. The undetected error probability decreases when the Hamming distance increases as we see in Figure 1.8; accordingly, for the selection of the CRC polynomial it is necessary to maintain high Hamming distance values. Hamming distance (HD) is defined by Koopman & Chakravarty (2004) as the minimum number of bit-errors that is undetectable, e.g. assume a polynomial with Hamming weights: 0 for 1-bit error, 0 for 2-bit errors, 452 for 3-bit errors, 0 for 4-bit errors and 356 for 5-bit errors; then HD = 3, since all 1 and 2-bit errors are detectable. In other words, the Hamming distance of a CRC polynomial is given by the first non-zero Hamming weigth.

Searching of the best design-SNRs Considering that our main goal is to decrease the detection latency of a block of symbols, the analysis for determining the design-SNRs should be under the frame or block-error-rate (BLER). We use the search algorithm, proposed by Vangala et al. (2015), for determining the best design-SNRs of construction methods. In our work, we analyze the performance of polar codes employing Bhattacharyya and Tal&Vardy constructions for different block lengths over AWGN channels. This means that for each pre-established block length using any given construction method, we determine the design-SNR for a range of SNRs or BLERs. The determination of the best design-SNR is carried out by comparing performance curves at several possible design-SNRs, which are obtained using extensive simulations. We also perform a comparison between performances of polar codes under Bhattacharyya and Tal&Vardy construction methods employing the obtained design-SNRs.

Following Vangala’s search-algorithm, first, we establish a set of design-SNRs of our interest. We consider a set of design-Eb/N0 equal to {0,1,…,10} in decibels (dB). Similar as Vangala’s work, we also consider a design-Eb/N0 = 1.42dB (design-Ec/N0 = -1.59dB), which is equivalent to the worst initial value (Z1(1) = 0.5) proposed by Arikan et al. (2008) for BEC channels. Constructions of polar codes at the set of design-Eb/N0 are performed with a fixed code rate, a fixed block length, and a particular method of construction. The design parameters used in our simulations are a code rate Rc = 0.5, block lengths N = {256,512,1024,2048}, and Bhattacharyya and Tal&Vardy construction algorithms. After extensive simulations, performances of polar codes are plotted as curves of BLER vs. Eb/N0, shown in Figures 2.1 and 2.2. We compare these performance curves and select one with the lowest BLER for a specific SNR or a range of SNRs of our interest. In particular, we select the performance curves with the lowest BLER for a relative low/medium range and a high range of SNRs, whose results are summarized in Table 2.1. The selected curves are highlighted with red and blue colors in Figures 2.1 and 2.2. Therefore, the design-SNRs of the selected curves are declared as the « best » designSNR for a specific range of SNRs under a fixed code rate and a fixed block length, either for Bhattacharyya or Tal&Vardy constructions.

Table des matières

INTRODUCTION
CHAPTER 1 THEORETICAL BACKGROUND
1.1 OFDM transmission scheme
1.2 Latency of a digital communication system
1.3 Reception latency of an OFDM system
1.4 Detection latency of an OFDM system
1.5 How to decrease latency?
1.6 Average detection latency
1.7 Error probability in the finite-blocklength regime
1.8 Sequential early detection
1.8.1 Multi-hypothesis sequential ratio test guided by list decoding
1.8.2 Sequential detection guided by error-detecting codes
1.9 Cyclic-redundancy-check codes
1.10 Selection of CRC polynomials
1.11 Polar Codes
1.12 Channel polarization
1.12.1 Channel Combining
1.12.2 Channel Splitting
1.12.3 Recursive channel transformation
1.13 Construction of polar codes
1.14 Polar Encoder
1.15 Successive-cancellation decoder
1.16 Decoding performance
CHAPTER 2 DESIGN-SNR FOR CONSTRUCTION OF POLAR CODES
2.1 Bhattacharyya-based construction
2.2 Tal & Vardy’s construction
2.3 Design-SNR of polar codes over AWGN channels
2.4 Searching of the best design-SNRs
2.4.1 Influence of the design-SNRs on polar code performance
2.4.2 Results
2.4.3 Error performance comparison under the best design-SNRs
2.5 Conclusion
CHAPTER 3 SEQUENTIAL EARLY DETECTION BASED ON CRCPOLAR CODES
3.1 Proposed scheme for decreasing the average detection latency
3.2 Implementation of the proposed scheme
3.3 Problem formulation
3.4 Basic setting of the early detection scheme
3.4.1 Assignation of bit channels
3.4.2 Bit-arrangement formats
3.4.3 Concatenated CRC-polar code without early detections
3.5 Selection of CRC polynomials
3.6 Performance of the early detection scheme with appropriate CRC polynomials
3.7 Selection of the initial detection time of sequential early detections
3.8 Performance of the early detection scheme with suitable IDTs
3.9 Statistical average latency of different detection distributions
3.10 Comparison of the statistical and simulated average latency
3.11 Is the latency reduction possible in practice?
3.12 Conclusions
CONCLUSION AND RECOMMENDATIONS
BIBLIOGRAPHY

Télécharger le rapport complet