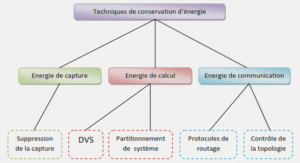
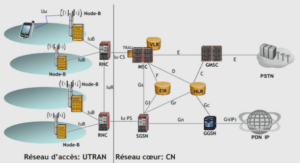
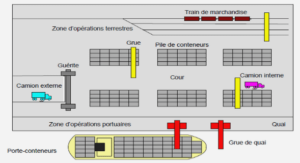
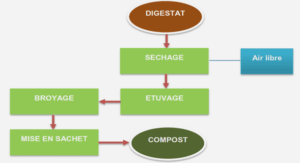
Deduction modulo
Deduction modulo was introduced by Gilles Dowek, Thérèse Hardin and Claude Kirchner in order to provide a logical framework where proving and computing are separated, in order to discriminate, in a proof, which parts are more efficiently performed by a processor: the computation; and which parts are more efficiently performed by a human: the (logical part of the) proof. The idea is to consider as equal, propositions which are computed equal by an external tool. This way, we only need one step of deduction to prove the proposition 2012 + 2012 = 4024, since an external processor can compute the term 2012 + 2012 into the term 4024. This formalism was introduced to build improved proof-assistants, which allow the human user to focus only on the parts of proofs which need human reasoning, and which can be faster in checking proofs, by using a external dedicated reliable program to compute on integers (or on other data types). Deduction modulo is a powerful logical framework, since it allows to express proofs of theories like arithmetic, simple type theory, some variants of set theory, and so on… The counter-part of this power, is that it allows to express theories which do not satisfy the cut elimination property or the strong normalization property. Hence we have to prove cut elimination or strong normalization for each theory that we want to prove consistent. Semantic methods were developed by Olivier Hermant to prove cut elimination for theories expressed in deduction modulo. On the other hand, Gilles Dowek and Benjamin Werner adapted the technique of reducibility candidates to deduction modulo, by defining the notion of pre-model which provides a sound criterion for strong normalization of theories expressed in deduction modulo. Later, Gilles Dowek exhibited the connection between semantic methods of building models and the apparently syntactic technique of reducibility candidates, by defining an extension of Heyting algebras, called Truth Values Algebras, pointing out one of these algebras corresponding to reducibility candidates, and deducing from his work with Benjamin Werner, that having a model valued in this algebra is a sound criterion for strong normalization of theories expressed in deduction modulo. However this criterion is not known to be complete. It could be that there exists strongly normalizing theories which do not satisfy this criterion.
Terms, propositions and inference rules
In this work, we present a version of Natural deduction based on a manysorted first-order language. We shall focus on minimal natural deduction, that is natural deduction with only the connective representing the implication and the universal quantifier.
Definition 2.1 ((Many-sorted first-order) language).
A language hT, F, Pi is the combination of a set T of sorts, a set F of function symbols which come with their ranks, and a set P of predicate symbols which also come with their ranks. Given an infinite set of variables of each sort, we define the set of terms associated to this language, as follows:
Definition 2.2 (Terms).
Given a language hT, F, Pi, the set of terms is defined inductively from variables.
• Variables of sort T are terms of sort T.
• If f is a function symbol of rank hT1, .. . ,Tn, Ui and t1, .. . ,tn are respectively terms of sort T1, .. . ,Tn, then f t1 . .. tn is a term of sort U. Propositions are built-up from predicates and terms with the connective ⇒ and the universal quantifier ∀. Notice that the quantification in ∀x.A is implicitly restricted over the sort of the variable x. Definition 2.3 (Propositions). Given a language hT, F, Pi, the set of propositions of minimal natural deduction based on this language is defined as follows:
• If P is a predicate symbol of rank hT1, .. . ,Tni and t1, .. . ,tn are respectively terms of sort T1, .. . ,Tn, then P t1 . .. tn is an atomic proposition.
• If A and B are two propositions, then A ⇒ B is a proposition.
• If A is a proposition and x is a variable, then ∀x.A is a proposition (we say that x is bound in A by the universal quantifier ∀ and we consider propositions equal modulo renaming of bound variables of the same sort).
Definition 2.4 (Free variables).
The set FV (t) of free variables of a term t is the set of variables which appear in t. For all propositions A, we define its set free variables FV (A) as the set of occurrences of variables which appear in A and which are not bound by a universal quantifier:
• FV (P t1 . .. tn) = FV (t1) ∪ . .. ∪ FV (tn)
• FV (A ⇒ B) = FV (A) ∪ FV (B)
• FV (∀x.A) = FV (A) − {x}
A proposition (resp. a term) is closed if it does not contain free variables.
Definition 2.5 (Substitution).
The substitution (t/x)t ′ of a variable x by a term t of the same sort (such that x does not appear free in t) in a term t′is defined by induction on the structure of t′ as:
• (t/x)y = t, if x = y and y otherwise
• (t/x)(f t1 . .. tn) = f (t/x)t1 . ..(t/x)tn
The substitution (t/x)A of a variable x by a term t of the same sort (such that x does not appear free in t) in a proposition A is defined by induction on the structure of A as:
• (t/x)(P t1 . .. tn) = P (t/x)t1 . ..(t/x)tn
• (t/x)(A ⇒ B) = (t/x)A ⇒ (t/x)B
• (t/x)(∀y.A) = ∀y. (t/x)A
Notice that we suppose here that x 6= y and y /∈ FV (t) (y has to be first renamed otherwise).
Cut elimination and normalization
Given the typing rules of minimal natural deduction, one can build different typing derivations which correspond to the same typing judgement. Hence one might wonder how to build a minimal tree giving the derivation of a typing judgement (for automated theorem proving, for example). And how to eliminate detours which may appear during the building of such typing derivations, detours which we call cuts. The notion of cut represents the introduction of an intermediate lemma in a proof, in order to use an instantiation of this lemma. Formally, a cut in a proof derivation is an elimination rule, whose main premise is the introduction rule of the same connective or quantifier
Rewrite rules versus axioms
In deduction modulo a theory is formed with a set of axioms and a congruence relation, often defined by a set of rewrite rules. For instance, when defining arithmetic in deduction modulo, we can either take the usual axiom ∀x. x + 0 = x or orient this axiom as a rewrite rule x+ 0 → x, preserving provability. In this case the rule rewrites the term x+0 into the term x. Another solution is to consider a rewrite rule on propositions as: x + 0 = x → A ⇒ A (where A is a proposition, since A ⇒ A is derivable in any context as we have seen in section 2.1.1). Axioms and rewrite rules play different roles in proofs and the structure of proofs is deeply affected when theories are expressed as rewrite rules. In particular, the cut elimination property may hold for one formulation of an axiom as a rewrite rule, but not for another one. Cut elimination is a much more powerful result (and hence more difficult to prove) when theories are expressed via rewrite rules: G. Burel has recently proved that cut elimination is an undecidable property in deduction modulo [8]. In particular, for axiom-free theories, cut elimination implies consistency as in minimal natural deduction,. Indeed, in the case of theories expressed with axioms, we cannot prove anymore that a cut-free proof always ends with an introduction rule, since it can use one of the axioms of the considered context. Whereas in axiom-free theories, we can still prove that all cut-free proofs in an empty context end with an introduction rule. Notice that when theories are expressed via inference rules, as in Superdeduction, we can neither prove that a cut-free proof always ends with an introduction rule, since it can use one of the introduced inference rules. Another important point is that deduction modulo permits to define a uniform notion of cut for all theories that can be presented by rewrite rules only. This notion of cut is the one we have defined in section 2.1.3 and subsumes that of Church’s simple type theory (also-called higher-order logic) since simple type theory can be defined as an axiom free theory modulo. More generally, it subsumes the notion of cut introduced by Prawitz [45] and used for various theories, in particular for set theory [10, 29, 3, 11, 22]. In chapter 3, we shall focus on rewriting and will consider theories expressed without axioms turned into inference rules. Moreover, we shall only consider theories expressed with rewrite rules on propositions (and not on terms). We shall see in section 2.2.3 how (minimal) simple type theory and arithmetic can be expressed this way in (minimal) deduction modulo.
About reducibility candidates
The main idea of reducibility candidates is to associate to each proposition A a set of proof-terms called RA containing only strongly normalizing terms and then prove the so-called adequacy lemma: if a proof-term π is a proof of A (there exists a context Γ such that Γ ⊢ π : A) then it is in RA and therefore strongly normalizing. In order to prove this adequacy lemma, we need that the sets RA satisfy other properties than containing only strongly normalizing proof-terms, as we shall see in the following. The proof of this adequacy lemma is done by induction on the length of the typing derivation Γ ⊢ π : A. Let us describe how it works for simply-typed λ-calculus (we consider natural deduction with only one connective : ⇒). We actually need a more precise formulation of the adequacy lemma as: if Γ ⊢ π : A then if σ is a substitution such that for all proof-variables α declared of type B in Γ, σα ∈ RB, then σπ ∈ RA (notice that in this case, if such a substitution σ exists, then π ∈ SN since σπ ∈ SN). In order to prove this statement, we reason by case on the last typing rule used in the typing derivation Γ ⊢ π : A.
• If this last rule is the rule axiom then π is a proof variable declared of type A in Γ therefore σπ ∈ RA by hypothesis.
• If this last rule is the rule ⇒-elim then π has the form π1π2 and we know, by induction hypothesis that there exists a proposition B such that σπ1 ∈ RB⇒A and σπ2 ∈ RB. In order to prove that σ(π1π2) is therefore in RA we suppose another property on the sets RC, for all propositions C: we suppose that for all propositions D and E, RD⇒E is exactly the set of proof-terms ρ such that for all ρ′in RD, ρρ′is in RE. Provided that the sets RC satisfy this property, we can conclude, in this case, that σ(π1π2) = σπ1 σπ2 ∈ RA.
• If this last rule is the rule ⇒-intro then π has the form λα.π1, A has the form B ⇒ C and we know, by induction hypothesis that for all ρ ∈ RB, (ρ/α)σπ1 ∈ RC. But we want that for all ρ ∈ RB, σ(λα.π1) ρ ∈ RC. We can notice that (ρ/α)σπ1 is a β-reduct of σ(λα.π1) ρ. This leads to make another assumption on the sets RD, for all propositions D: we suppose that if a proof-term is neutral and all its β-reducts are in RD then it is also in RD (notice that we make an assumption on all β-reducts of a neutral proof-term, not on only one β-reduct, since we want this property to be adequate for strong normalization and not for weak normalization). Then, in order to prove that σ(λα.π1) ρ is in RC we reason on the sum of maximal lengths of reductions sequences from σ(λα.π1) and ρ which are both strongly normalizing since they belong to RB⇒C and RB respectively. If the considered β-reduct of σ(λα.π1) ρ is (ρ/α)σπ1, we can conclude by induction hypothesis on the length of the typing derivation. Otherwise, in order to be able to conclude by induction hypothesis on the maximal lenghts of reductions sequences if the β-redex reduced in σ(λα.π1) ρ appears either in σ(λα.π1) or ρ, we have to make a last assumption on the sets RD, for all propositions D: they are stable by β-reduction.
|
Table des matières
1 Introduction
2 Proof normalization as a model-theoretic notion
2.1 Natural deduction
2.1.1 Terms, propositions and inference rules
2.1.2 Proof-terms and typing rules
2.1.3 Cut elimination and normalization
2.2 Minimal deduction modulo
2.2.1 Rewrite rules versus axioms
2.2.2 Definition
2.2.3 Theories expressed in minimal deduction modulo
2.3 Reducibility candidates
2.3.1 About reducibility candidates
2.3.2 Pre-models for deduction modulo
2.4 Truth values algebras
2.4.1 Definition
2.4.2 Models valued in truth values algebras
2.4.3 C, the TVA of reducibility candidates
3 Sound and complete semantics for strong normalization in minimal deduction modulo
3.1 Are usual reducibility candidates complete ?
3.1.1 About the (CR3) property
3.1.2 The problem of neutral normal proof-terms
3.1.3 How to interpret the universal quantifier
3.1.4 Language-dependent truth values algebras
3.2 Well-typed reducibility candidates
3.2.1 C≡ , the LDTVA of ≡-well-typed reducibility candidates
3.2.2 C≡ -models as a sound semantics for strong normalization
3.2.3 C≡ -models as a complete semantics for strong normalization: the long way
3.2.4 C≡ -models as a complete semantics for strong normalization: the short way
3.3 Theory-independent sound and complete reducibility candidates
3.3.1 The main idea
3.3.2 C′, yet another algebra of reducibility candidates
3.3.3 Soundness of non-empty C′-models
3.3.4 Defining a function from C≡ to C′
3.3.5 Proving that this function is a morphism
3.3.6 Completeness of non-empty C′-models
3.4 Conclusion
4 Sound and complete semantics for λΠ-modulo
4.1 The λΠ-calculus
4.1.1 Syntax of the λΠ-calculus
4.1.2 Typing rules of the λΠ-calculus
4.2 The λΠ-calculus modulo
4.2.1 Syntax of the λΠ-calculus modulo
4.2.2 Typing rules of the λΠ-calculus modulo
4.2.3 Technical lemmas
4.3 Pre-models for λΠ-modulo
4.3.1 Definition of pre-models
4.3.2 Soundness of pre-models for strong normalization
4.3.3 An example of pre-model
4.3.4 Completeness of pre-models for strong normalization
4.4 Conclusion
5 Embedding functional Pure Type Systems in λΠ-calculus modulo
5.1 The Pure Type Systems
5.2 Embedding functional Pure Type Systems in the λΠ-calculus modulo
5.2.1 Definition
5.2.2 Soundness of the embedding
5.3 How to prove strong normalization of the embedded theories in λΠ-calculus modulo
5.4 Conservativity of the embedding
5.4.1 Confluence of λΠP -calculus modulo
5.4.2 Which notion of conservativity?
5.4.3 Back translation
5.4.4 Getting rid of weak η-long forms
5.5 Implementation
5.6 Conclusion
6 Conclusion and perspectives
6.1 Summary
6.2 Future work
6.2.1 Toward a sound and complete semantics for strong normalization in Pure Type Systems
6.2.2 Weak and Strong normalization
6.3 Conclusion
Bibliography
Index of definitions
![]() Télécharger le rapport complet
Télécharger le rapport complet