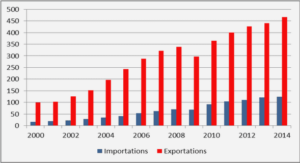
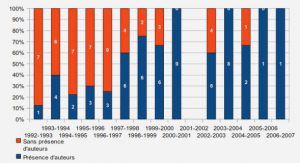
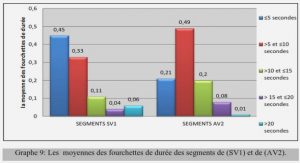
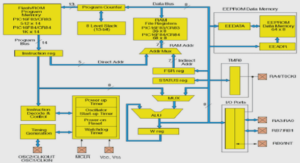
Location models
A number of empirical studies suggest variables that play a significant role in influencing the establishment’s location choice. We briefly describe those which are most relevant. According to Arauzo-Carod (2005) and Maoh (2005), an establishment will decide to enter a market if it detects a potential business opportunity and if the capital and human resources are available. An establishment must choose a type of activity that reflects both its technological and organizational level and its minimum size. With these parameters in mind, the establishment makes a decision as to where to locate. Since choosing a particular area in which to locate is critical to the establishment’s success or failure (Strotmann, 2007), the main task of the establishment is to identify the places which offer the highest possible potential profit. Local economic climate in terms of its ability to attract new entrants, as well as the structure of establishments at the local level are other factors that can influence the decision (Liviano-Solís and Arauzo-Carod, 2014). Locations with lower input costs are also more likely to experience a higher number of births of new establishments (Rocha, 2008).
Sutton (2007) notices that ranking sectors according to the degree of (entry-exit) turbulence appears to offer similar results across countries, suggesting that there are some sectorspecific factors at work in molding this pattern. Rocha (2008) and Liviano-Solís and ArauzoCarod (2014) concur, finding that local employment density attracts new entrants in related sectors and has a positive impact on the establishment’s productivity. However, when this density is too high, the effect becomes negative due to congestion costs, including for example, high land prices and costly commuting. This results in an inverted U-shape profile between the effect of concentration of economic activity and site attractiveness. The relationship is initially positive, but becomes negative after a certain threshold is crossed. Maoh and Kanaroglou (2005, 2007) state that agglomeration effects tend to be more significant in particular activity sectors, such as retail and services.Local authorities try to offer different incentives in a bid to attract establishments to less developed areas and accelerate the development of the whole region. These include, but are not limited to, supply of infrastructure, designation of new building zones, and tax reductions.
Empirical results from various studies undertaken in different countries worldwide demonstrate that these policies may have positive, negative, or neutral effects on the location choice and activity distribution.
Spacial effects in the context of establishment location choice
Establishment location choice has attracted considerable attention in the past decades (see, e.g., a survey of Arauzo-Carod et al., 2010). The objective of the studies on location of establishments is the analysis of the determinants of how the choices are being made. Distance plays usually only a secondary role in the estimation. Only recently has the importance of spatial effects been emphasized in this context. Despite the existence of spatial effects, there is a little mention in the literature of previous attempts to incorporate spatial effects in establishment or firm location decision-making processes (Bhat et al., 2014; Buczkowska and Lapparent, 2014; Liviano-Solís and Arauzo-Carod, 2013; Liesenfeld et al., 2015; Lambert et al., 2010; Klier and McMillen, 2008).
Klier and McMillen (2008) build a model with a spatially weighted dependent variable to analyze location decisions of auto supplier plants in the US (discrete choice framework).
They account for the clustering tendency assuming that the location of a plant in a particular county depends on the location of plants in contiguous counties. Lambert et al. (2010) develop the Spatial Autoregressive Poisson model and assess the use of a two-step limited information maximum likelihood approach. This model includes a spatially lagged dependent variable as a covariate. The proposed estimator models the location events of start-up firms in the manufacturing industry as a function of neighboring counts. Effects of location determinants can be divided into direct, indirect, and induced effects thus providing information to better understand regional patterns. Liesenfeld et al. (2015) propose a maximum likelihood (ML) approach based on the spatial efficient importance sampling applied to the spatial Poisson and negative-binomial models for manufacturing establishment location choices. ML estimation of parameter-driven count data models requires high-dimensional numerical integration. Bhat et al. (2014) formulate a spatial multivariate model to predict the count of new industrial businesses at a county level in the state of Texas. It allows for a better recognition of the industry specific determinants. The authors accommodate overdispersion and excess zero problems. They account for the unobserved factors that simultaneously affect the county-level count of new businesses in different sectors and spatial dependence effects across counties. Dubé et al. (2016) use a discrete choice model to describe the individual business location choices in the nonmetropolitan area in Canada demonstrating that the final decision of an establishment should be related to the surrounding economic landscape.
Distance measures
The use of the Euclidean distance is widespread in economics (e.g., Duranton and Overman, 2005; Partridge et al., 2008). This metric is known to all and experienced by all in everyday life, hence a prime candidate to capture economic interactions. According to Guy (1983), the use of straight-line distance to represent a travel function is unsatisfactory, however, though it does simplify computations. In the same line, Combes and Lafourcade (2003,2005) claim that the Euclidean distance can only be regarded as a simplistic measure of the actual physical distance. The curvature of the Earth is the first source of systematic error. When calculating the straight-line (crow fly) distance between two remote points, the Euclidean distance may be replaced by the great circle distance, which takes the Earth’s spherical shape into account (Axhausen, 2003). The second source of systematic error comes from the fact that in practice, people (or goods) rarely move from point A to point B along a straight line as assumed in the Fetter’s ”Law of Markets” (1924). For instance, car users may only drive on the existing road network, hence the well-known example of the Manhattan distance (Eaton and Lipsey, 1980). As the road network plays a central role in most urban transportation systems around the world, the Euclidean metric would therefore be inappropriate for the study of intra-urban location (Eaton and Lipsey, 1980; Perreur and Thisse, 1974).
Talen and Anselin (1998) suggest that distance can be computed in a variety of ways and use the actual street network in their empirical study of public facilities locations. Distance is measured by the means of a shortest path algorithm between the centroids of census tracts and the coordinates of public facilities of interest. They consider the shortest path network distance to be more relevant than the straight-line distance regarding the analyzed issue. Actual driving distances and travel times over a road network are perceived also by Boscoe et al. (2012) to be superior and substantially more precise than the straight-line distance. Previously, these metrics were considered as an expensive and labor-intensive to obtain. Nowadays, the commercial websites, such as Google, Yahoo!, Mapquest, Bing, Rand McNally, Michelin of fer precise driving directions between nearly all locations in the developed world (Boscoe et al., 2012; Le Gallo and Dall’erba, 2008).
Motivation of model choice
The Paris region is highly heterogeneous, especially regarding economic activity. While few municipalities host a large number of new establishments, others struggle to be chosen by any, and a large group of municipalities is left with no new entries. Based on the data for the Paris region aggregated at the municipality level, depending on the analyzed sector, the percentage of municipalities left with no new creation ranges from 34% up to 61%. The number of municipalities left with zero new entries in the construction sector equals to 439, in the real estate activities sector to 738, and in the special, scientific, technical activities sector to 569 out of 1300 possible municipalities that met no new establishments. These findings are similar to the remark made by Liviano-Solís and Arauzo-Carod (2014) based on the analysis of the Catalan data. The authors state that the distribution of entries is heavily skewed: a small group of municipalities meet the largest number of entries, while more than a half receive no entries at all. Municipalities range from small isolated villages in rural areas to huge and densely populated cities.
When the observed data display a higher fraction of zeros than would be typically explained by the standard count data models, the zero inflated or hurdle models can be suggested. This paper seeks to address the complaint voiced by Liviano-Solís and Arauzo-Carod (2013) and Bhat et al. (2014) who notice that heretofore scholars have not fully explored the hurdle model technique when analyzing location phenomena. It is thereby in line with Liviano-Solís and Arauzo-Carod (2013) and Buczkowska and Lapparent (2014). In contrast to the two previous works, which focus on determining which type of model (Poisson, negative binomial, zero-inflated versions of these models, hurdle-Poisson, and hurdle negative-binomial) best fits their data, this paper focuses instead on the issue of which type(s) of spatial representation(s) best characterizes spatial spillovers. Considering all these points, a discrete mixture of hurdlePoisson models is developed, wrapping the spatial metrics in a common statistical framework of analysis.
Within-industry and inter-industry interactions
An establishment does not seem to act in isolation during its decision-making processes (Nguyen et al., 2012). Jayet (2001) proves the existence of interactions among units located in space. Interactions of agents may occur in various forms and with various levels of magnitude. A long discussion on within-industry economies (own-industry competition effects versus Marshallian agglomeration economies, i.e., own-sector collocation), and inter-industry economies (Jacobsian agglomeration economies, i.e., economic diversity) can be found in the existing literature. A number of empirical methods to quantify and characterize the tendency of individual establishments or industries to cluster or disperse in space have been proposed.
These measures can be divided into three groups: empirical measures, such as Herfindahl or Gini indices which do not take space into account (see, e.g., Krugman, 1991); indicators, such as Ellison and Glaeser index (Ellison and Glaeser, 1997) which uses space as being discrete (administrative units); and measures that treat space as being continuous (e.g., Duranton and Overman, 2005; Casanova et al., 2017).
Yet, instead of analyzing spatial distribution of economic activities, e.g., concentration or dispersion tendencies of pre-existing establishments that belong to two industries, horizontally or vertically linked, we rather opt to explain how the actual and potential presence of other establishments from both, the same and other sectors, influence the location decisions of new units. The interrelated nature of locational decisions suggests modeling them as strategic games to recognize the interdependence of payoffs and actions.
The impact on payoffs due to the behavior of other establishments is a vector that contains the number of establishments in each location in the market (Seim, 2006). In addition, since establishments have different costs, sell different products, they seem to care about the actual identities of other players rather than simply the total number of establishments. It is therefore important to explore how these potential heterogeneities might affect estimation (Berry and Reiss, 2007). In the paper by Seim (2006), profits depend only on the number of entrants at every location and not on the entrants’ identities. Seim (2006) maintains sym metry for computational reasons suggesting that more heterogenous payoff functions can be proposed instead. To cope with this problem, Zhu and Singh (2009) propose a modeling approach that explicitly allows for asymmetries related to identity of establishments. Clearly, allowing for such establishment asymmetries is not without cost since it leads to a significantly larger number of parameters to be estimated (Zhu and Singh, 2009).
|
Table des matières
Contents
1 General introduction
1.1 Location choice models of establishments
1.2 Key questions
1.3 Relevance of research
1.4 Literature
2 Location choices of newly-created establishments: Spatial patterns at the aggregate level
2.1 Introduction
2.2 Review of empirical literature
2.3 Study area
2.4 Data
2.5 Descriptive statistics
2.6 Parametric models
2.7 Results
2.8 Conclusions
3 Euclidean versus network distances: A mixture model of the intra-metropolitan location choice of establishments
3.1 Introduction
3.2 Literature review
3.3 Data
3.4 Model
3.5 Results
3.6 Conclusions
4 Location choices under strategic interactions: Interdependence of establishment types
4.1 Introduction
4.2 Within-industry and inter-industry interactions
4.3 Why bother about strategic interactions?
4.4 Push and pull factors
4.5 Data
4.6 Model
4.7 Results
4.8 Conclusions and possible applications
5 Locational strategies of multi-store firms: A daytime population
5.1 Introduction
5.2 Literature review
5.3 Data
5.4 Market description
5.5 Nearest neighbor distance
5.6 Model: Reduced-form profit function
5.7 Empirical results
5.8 Conclusions
6 Concluding remarks
6.1 Main findings
6.2 Practical recommendations
6.3 Future research directions
![]() Télécharger le rapport complet
Télécharger le rapport complet