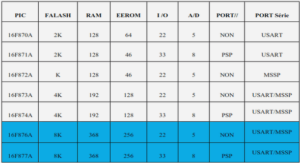
EVALUATION OF GENOTYPIC DIVERSITY MEASUREMENTS EXPLOITED IN REAL-CODED
EEB concept
The EEB can be viewed in terms of one of two paradigms (Gupta, Smith, and Shalley, 2006):
1) exploration and exploitation act as opposing forces, where increasing one reduces the other; or 2) they can be considered as orthogonal forces. This second perspective offers the possibility of increasing both exploration and exploitation simultaneously.
Consequently, monitoring the EEB must involve two metrics: one for the exploration axis, and one for the exploitation axis. Exploration is best described by the genotypic formulation, as it summarizes the distribution of the individuals over the search space, while exploitation is best characterized by phenotypic formulations, as promising regions are targeted based on fitness information. With normalized evaluation, unitary genotypic and phenotypic values relate to maximum exploration and exploitation respectively.
According to this framework, exploration increases with a rise in genotypic diversity. In contrast, exploitation corresponds to the intensification of phenotypic convergence. To avoid confusion, we will refer to the phenotypic convergence measure (PCM) instead of the PDM when dealing with the EEB framework.
Review of phenotypic formulations
For any landscape structure, the orthogonal EEB framework portrays the way resources are allocated, and, consequently, optimizer performance. In fact, the use of a phenotypic formulation is only justifiable from this perspective. To reduce computational effort, some researchers only consider phenotypic diversity (the EEB concept of opposing forces), on the assumption that fitness differences reflect genotypic space diversity (Motoki, 2002). This is a limitation, however, and few researchers using this approach take it into account (Neri, Toivanen, and Mäkinen, 2007; Caponio et al., 2007; Tirronen and Nerri, 2009; Friedrich, Hebbinghaus, and Neumann, 2009). The following scenario illustrates the problem: A population of N individuals located on N different peaks of the same magnitude would be considered to be in a state of convergence from the phenotypic point of view, whereas from a genotypic perspective, the diversity would be clearly visible. Therefore, in the presence of an unknown landscape structure, relying solely on phenotypic measurement could be misleading in the search performance analysis.
Requirements for a suitable diversity measure
In pioneering research, Weitzman (1992) listed 14 principal characteristics of reliable diversity measures. Weitzman acknowledged that these properties are not equally important.
Later, Solow and Polasky (1994) identified three of them as natural requirements:
1. Monotonicity in species: adding a species (or individuals, in the current context) should not decrease diversity or DP DP ( ‘) ( ) ≤ , if P’ is a subset of population P.
2. Twinning: the addition of an individual or a species already in the population should not increase the diversity or DP i DP ( ) () ∪ = , if di j ( , ) 0, = where and jP iP ∈ ∉ .
3. Monotonicity in distance: an unambiguous increase in distance between individuals should be reflected in the measurement or DP DP ( ‘) ( ) ≤ , if di j di j ( ‘, ‘) ( , ) ≤ .
The ideas governing these requirements apply to phenotypic measurement. In reality, the diversity measurement should be understood as a description of the coverage of the search space. This concept is completely and rigorously expressed by those diversity requirements.
Nevertheless, the three requirements must first be reformulated in terms of fitness distribution.
Validation framework for the requirements analysis
Six deterministic cases of frozen fitness diversity are proposed to evaluate and illustrate the phenotypic formulation responses, as follows:
Case 1: All the individuals are located at fbest.
Case 2: 50% of the population is located at the mid-point between fworst and fbest, while the remaining portion is at fbest.
Case 3: N-1 of the population is located at the mid-point between fworst and fbest, while the remaining individual is at fbest.
Case 4: 50% of the population is located at fworst, while the remaining portion is at fbest.
Case 5: N-1 of the population is located at fworst, while the remaining individual is at fbest.
Case 6: The individuals are uniformly distributed over a predefined fitness range (VMD case).
The first case corresponds to a converged situation. Cases 2 and 3, and Cases 4 and 5 present equivalent phenotypic diversities. However, Cases 4 and 5 present higher diversities than Cases 2 and 3. Furthermore, Cases 2 to 5 have low phenotypic diversity (two fitness values).
In contrast, Case 6 corresponds to the highest phenotypic diversity state.
New phenotypic formulation proposed
To control the EEB within the orthogonal framework, a reliable PCM is required. The previous section revealed that no phenotypic formulation available in the literature offers a perfect description of the scattering of the fitness distribution.
This new formulation is based on multiplication of the phenotypic value differences established between neighbors. Once the fitness distribution has been sorted, the computation can start from any side of the sorted distribution. The formulation ensures that the state of maximum phenotypic diversity occurs when all the individuals are uniformly spread out within the fitness range, which leads to the VMD case and fulfillment of the monotonicity in fitness varieties requirement.
Analysis of PCMs over specifically designed landscapes
Now that the new phenotypic formulation has been proved to perform in accordance with the diversity requirements, this section examines its behavior over the course of a search process.
PCM1 to PCM12 are also included in the investigation. However, this analysis requires that the phenotypic state be known quantitatively, or at least qualitatively, throughout the optimization process. This would become a serious issue if the search were based on an EA, since the sampled fitness distribution depends on the search path followed, which is a stochastic process. The result would be to hide the phenotypic distribution structure of a chosen benchmark. Furthermore, replications of the simulations, which are essential for validating the reliability of a PCM, would be useless.
In order to circumvent this problem, a generic benchmark is proposed to ensure uniform fitness distribution sampling, as well as control of the phenotypic states by the landscape definition and the search dynamic. Furthermore, with this benchmark, no genetic operator is involved in the evolution of the population. Instead, at each iteration, a new fitness distribution is sampled over the landscape. Phenotypic convergence is simulated by reducing the sampling boundary as the process evolves. Consequently, the process begins in a ful phenotypic diversity state (PCM = 0) and proceeds to a convergence state (PCM = 1) following a predefined schedule. As a result, the phenotypic distribution is known throughout the evolution process.
|
Table des matières
INTRODUCTION
0.1 Background
0.2 Research problem
0.3 Objective
0.4 Organization
CHAPTER 1 REVIEW AND STUDY OF GENOTYPIC DIVERSITY MEASURES FOR REAL-CODED REPRESENTATIONS
1.1 Introduction
1.2 Genotypic diversity measure
1.2.1 General concept
1.2.2 Normalization
1.2.3 Genotypic diversity measures
1.2.4 Prior observable flaws on certain GDMs
1.3 Review of comparative studies
1.4 Benchmark
1.5 Results
1.5.1 Unimodal landscape experiment
1.5.2 Multimodal landscape experiment
1.5.3 Stability analysis
1.5.4 Sensitivity analysis
1.5.5 Effect of outliers
1.6 GDM comparison over the CEC’05 benchmark
1.7 Discussion
1.8 Conclusion
CHAPTER 2 EVALUATION OF GENOTYPIC DIVERSITY MEASUREMENTS EXPLOITED IN REAL-CODED REPRESENTATION
2.1 Introduction
2.2 Problem statement
2.3 Characterizing population diversity
2.4 Validation of the representative GDMs
2.4.1 Reduced population arrangement
2.4.2 Controlled cases of population diversity
2.4.3 Discussion
2.5 Conclusion
CHAPTER 3 REVIEW OF PHENOTYPIC DIVERSITY FORMULATIONS FOR DIAGNOSTIC TOOL
3.1 Introduction
3.2 EEB concept
3.3 Review of phenotypic formulations
3.3.1 General concept
3.3.2 Normalization
3.3.3 PCM formulation
3.4 Validation of phenotypic formulations
3.4.1 Requirements for a suitable diversity measure
3.4.2 Validation framework for the requirements analysis
3.4.3 Relevance of the phenotypic formulations
3.5 New phenotypic formulation proposed
3.5.1 Analysis of the new phenotypic formulation over the diversity requirements
3.6 Analysis of PCMs over specifically designed landscapes
3.6.1 Linear function
3.6.1.1 Landscape definition
3.6.1.2 Behavioral results of the PCMs
3.6.2 Double-slope landscape
3.6.2.1 Landscape definition
3.6.2.2 Behavioral results of the PCMs
3.6.3 Saw tooth landscape
3.6.3.1 Landscape definition
3.6.3.2 Behavioral results of the PCMs
3.7 Assessment of desirable PCM qualities
3.7.1 Definition of desirable PCM qualities
3.7.2 PCM13 reliability analysis
3.7.3 PCM13 sensitivity analysis
3.7.4 PCM13 analysis with outliers
3.8 Application of the EEB diagnostic tool
3.9 Conclusion
CHAPTER 4 EVALUATION OF THE GENERALIZED PHENOTYPIC FORMULATION AS A GENOTYPIC DIVERSITY MEASURE
4.1 Introduction
4.2 Generalization of PCM13 as multivariate diversity measure
4.3 Performance evaluation of the proposed GDM
4.3.1 Validation framework
4.3.2 Unimodal landscape experiment
4.3.3 Multimodal landscape experiments
4.3.4 Desirable quality criteria
4.3.4.1 Repeatability
4.3.4.2 Robustness
4.3.4.3 Influence of outliers
4.4 CEC’05 benchmark GDM comparison
4.5 Conclusion
CHAPTER 5 BAYESIAN NETWORK AS AN ADAPTIVE PARAMETER SETTING APPROACH FOR GENETIC ALGORITHMS
5.1 Introduction
5.2 Review of adaptive parameter control strategies
5.2.1 Parameters involved
5.2.2 Feedback indicators
5.2.3 Credit assignment scheme
5.2.4 Parameter selection rule
5.2.4.1 Heuristic rule
5.2.4.2 Fuzzy Logic Controller (FLC)
5.2.4.3 Probability Matching (PM)
5.2.4.4 Adaptive Pursuit (AP)
5.2.4.5 Multi-Armed Bandit (MAB)
5.2.4.6 Covariance Matrix Adaptation (CMA)
5.2.5 Discussion
5.3 Parameter adaptation through Bayesian network
5.3.1 Graphical model of BNGA
5.3.2 Credit assignment schemes
5.3.3 Conditional Probability Table (CPT)
5.3.4 BNGA process
5.4 Comparative study
5.4.1 Methodology
5.4.2 Parameter states involved
5.4.3 Hyperparameter sensitivity analysis
5.5 Results
5.5.1 Results of the SSGA parameter setting approaches
5.5.2 Results of the EA parameter setting approaches
5.6 Concluding discussion
CONCLUSION
![]() Télécharger le rapport complet
Télécharger le rapport complet