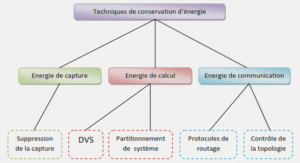
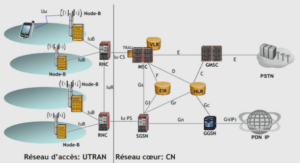
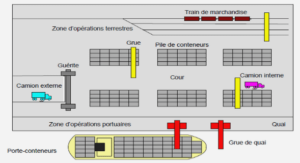
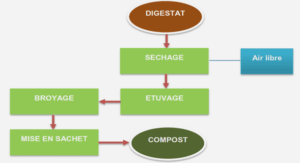
Dynamic changes in the environment, learning from scratch and on the fly
In many applications, especially with the raise of the use of internet, the environment that the machine intends to find description in is changing dynamically and many new data occur in it, see Figure 0.2. To keep the predictions about the states of the environment up-to-date, it is best to adapt to all these changes once they come to happen. One option is to wait for sufficient amount of data and then use these along with the old data to retrain the model of the environment. This is the approach of traditional offline models that require to learn the whole model from the beginning. This requires significant amount of time for the delay of the system to be used for predictions. A better option seems to be to update the model every time there is a change in the state of the environment and to be able to accommodate new structures of the data in the model. Many known offline models require, by definition, initialization of the number of the structures in the data and use methods such as cross-validation to determine these in case they are not known. This seems to be a problem for many online models, since the number of the classes needs to be set ahead and thus there is no possibility for learning on the fly.
Accuracy vs. Processing time For many applications, the use of online learning is purposed to be real-time, when the response or the prediction of the system to the environment needs to be fast. Furthermore, the use of incremental learning for offline learning is due to the saving of the processing time, when classical batch learning is too slow. Thus, in online and also incremental learning models, the machine needs to rely on simple updates that are fast, but also result into accurate predictions. In parametric learning a distribution of the data is assumed, such that this distribution is described by the parameters. Usually, an expected value, such as the mean is used accompanied with a variance or a covariance. By comparing these two we can see, that in univariate distributions, the mean and variance ignore covariances among the data as well as the variances for each dimension separately. There are methods, such as Naive Bayes, that take into account the variances within each dimension, but still lack the covariances. In some application this might not be an issue and the models based on univariate distributions can benefit from the low computational cost. But in many other applications a covariances between variables carry information that can be crucial for the whole learning and prediction process. On the other hand, introducing covariance brings increased computational cost, which can be detrimental for the real-time processing.
Forgetting
Since online learning relies on small updates and at each time step uses only sample of size one, the system cannot look at the data as a whole. Thus, instead of extracting the statistics from the whole sample, we assume that by these small updates we will converge to the expected value. Usually we need to set a rate at which the system learns or adapts to the new input. This rate tells us how agile the learning is. Setting this is an issue of stability-plasticity dilemma. We need to be able to decide, whether we want to rely on all data already known, making more stable decisions, or whether we want to be agile and flexible by adapting to the new state of the environment. In other words, ideally we want to avoid learning an unimportant event that brings only noise to the data, but at the same time be able to adapt to an important event. This dilemma goes hand in hand with the problem of forgetting. In online learning, the data stream continues and the old samples are usually not revisited. In multi-class problems, there are two basic strategies how to transform two-class models into multi-class establishment, and this is by keeping the true class as the positive class and either letting all the other classes as negative classes (one vs all) or doing pairwise models by choosing always only one other class as the negative class, and doing this for all possible combinations (one vs one). Either way, if one class is not used for a longer period of time, it becomes sparse compared to the other class/classes and basically is overrun by the negative examples, see Figure 0.3. This shifts the decision boundary so that the positive class is not longer recognizable.
Parameter-free modeling
One of our motivations is to be able to build user-friendly model, that is capable of adapting to new situations and to respond to them adequately, with as little human/users involvement as possible. This results into the need of being able to adapt to data that has not been seen ahead and our knowledge of the environment is restricted to the task the system is coping with. For example, in handwritten gesture recognition all we know is that the data are going to be handwritten gestures, but we do not know how they will look like, how many classes there will be or when they will be added to the system. We cannot say for sure how fast the system needs to learn, because we do not know how the environment will change in the future. We cannot rely on cross-validation, because we cannot rely on previously learned model. Thus, it is essential to avoid free/hyper parameters and let the model to adapt to the environment itself, using only the knowledge that will not change in time (i.e. the application). Many models rely on hyper parameters and the expertise of the teacher to be able to set these parameters. But this does not fit to the nature of online learning, and thus models that are able to adapt themselves are in need for many online learning based applications.
Online dimensionality reduction
The curse of dimensionality can be detrimental to the machine learning solution. While in some cases, the problem lies in the number of dimensions being higher than the number of data points, in other cases the high dimensionality can result into over-fitting, and thus high variance as well as computational complexity of the learning and recognition processes. In both cases, feature selection techniques are used, where a smaller number of features is chosen to be the ones representative enough. One group of techniques dealing with feature selection is dimensionality reduction techniques and in this section we describe Principal Component Analysis, where the principal components are updated in an incremental manner. Incremental Principal Component Analysis Principal Component Analysis (Hotelling, 1933) is an unsupervised projection method aiming to minimize the loss of information after mapping of the data X to a new space Z and maximize the variance within the data. The Ware the principal components, that the data X is projected onto, where after this projection the data Z are obtained such that on the first dimension of W the data have the highest variance, on second principal component they have the second highest variance, etc.
|
Table des matières
INTRODUCTION
0.1 Context of the thesis
0.2 Problem statement
0.2.1 Dynamic changes in the environment, learning from scratch and on the fly
0.2.2 Accuracy vs. Processing time
0.2.3 Forgetting
0.2.4 Parameter-free modeling
0.2.5 Missing data
0.3 Contributions
0.4 Outline of the thesis
CHAPTER 1 LITERATURE REVIEW
1.1 Online learning methods
1.1.1 Online linear methods
1.1.1.1 Stochastic gradient descent
1.1.1.2 Recursive Least Squares
1.1.2 Online clustering methods
1.1.2.1 Online k-means
1.1.2.2 Adaptive Resonance Theory
1.1.3 Online dimensionality reduction
1.1.3.1 Incremental Principal Component Analysis
1.1.4 Online kernel models
1.1.4.1 Incremental Support Vector Machine
1.1.5 Online ensemble models
1.1.5.1 Online AdaBoost
1.1.5.2 Evolving Neuro-Fuzzy models
1.1.5.3 Online Random Forest
CHAPTER 2 GENERAL METHODOLOGY
2.1 Objective of the research
2.1.1 Sub-objective 1: Develop online learning model tackling learning
on the fly and from scratch along with the accuracy vs. processing time problem
2.1.2 Sub-objective 2: Tackle forgetting of unused classes for online learning models and apply
2.1.3 Sub-objective 3: Develop online learning model able to work without free parameters
2.1.4 Sub-objective 4: Tackle the problem of missing data
2.2 Methodology
2.2.1 Incremental Similarity
2.2.2 Elastic Memory Learning
2.2.3 Self-Organized Incremental Model
2.2.4 The problem of missing data
CHAPTER 3 INCREMENTAL SIMILARITY FOR REAL-TIME ON-LINE INCREMENTAL LEARNING SYSTEMS
3.1 Abstract
3.2 Introduction
3.3 Related works
3.4 Incremental similarity
3.4.1 Euclidean and Mahalanobis distances
3.4.2 Our novel Incremental Similarity measurement
3.5 Models
3.5.1 ETS
3.5.2 ETS+
3.5.3 Incremental fuzzy model (IFM)
3.5.4 ARTIST: ART-2A driven rule management in TS model
3.5.5 K-means
3.6 Results
3.7 Conclusion and discussion
CHAPTER 4 ELASTIC MEMORY LEARNING FOR FUZZY INFERENCE MODELS
4.1 Abstract
4.2 Introduction
4.3 Related works
4.4 Recursive Least Squares for TS fuzzy models
4.5 EML: Elastic Memory Learning
4.6 EML+
4.7 Results
4.8 Conclusion and discussion
CHAPTER 5 SO-ARTIST: SELF-ORGANIZED ART-2A INSPIRED CLUSTERING FOR ONLINE TAKAGI-SUGENO FUZZY MODELS
5.1 Abstract
5.2 Introduction
5.3 Related works
5.4 ARTIST: ART-2A driven generation of rules for TS fuzzy models
5.4.1 Rule organization
5.4.2 Antecedent part
5.4.2.1 Incremental similarity measurement
5.4.3 Consequent part
5.4.3.1 Competitive Recursive Least Squares
5.5 SO-ARTIST: Self-Organized ART-2A based management of rules for TS fuzzy models
5.5.1 Merging the rules
5.5.1.1 Similarity measurement
5.5.1.2 Rule distance measurement
5.5.1.3 Merging membership parameters
5.5.1.4 Merging CCL parameters
5.5.1.5 Merging rule parameters
5.5.2 Splitting and discarding the rules
5.5.2.1 Dissimilarity, error and age measurement
5.5.2.2 Class distance measurement
5.5.2.3 Splitting membership parameters
5.5.2.4 Splitting consequent parameters
5.5.2.5 Splitting rule parameters
5.5.3 Self-Organized mechanism
5.5.3.1 Learning the learning rate
5.5.3.2 Learning the vigilance parameter
5.5.3.3 Merging process
5.5.3.4 Splitting process
5.5.3.5 Discarding process
5.5.3.6 Algorithm
5.6 Results
5.6.1 Self-Organization evaluation
5.6.1.1 Self-Organized framework evaluation
5.6.1.2 Evolution of Vigilance parameter and Learning rate
5.6.2 Accuracy evaluation
5.6.3 Learning without forgetting
5.7 Conclusion and Discussion
CHAPTER 6 FORGETTING OF UNUSED CLASSES IN MISSING DATA ENVIRONMENT USING AUTOMATICALLY GENERATED DATA: APPLICATION TO ON-LINE HANDWRITTEN GESTURE COMMAND RECOGNITION
6.1 Abstract
6.2 Introduction
6.3 Related works
6.4 Sigma-lognormal model
6.5 ARTIST
6.6 EML: Elastic Memory Learning
6.7 Framework for on-line real-time learning using synthetic data
6.8 Experiments
6.8.1 Experimental setting
6.8.2 Results
6.9 Conclusion and Discussion
CHAPTER 7 GENERAL DISCUSSION
7.1 Incremental Similarity
7.2 Elastic Memory Learning
7.3 Self-Organized incremental model
7.4 The problem of missing data
CONCLUSION AND RECOMMENDATIONS
BIBLIOGRAPHY
![]() Télécharger le rapport complet
Télécharger le rapport complet