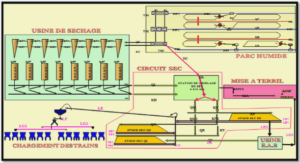
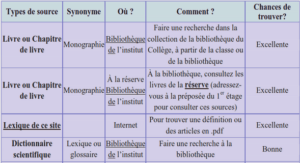
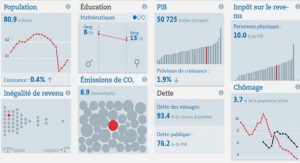
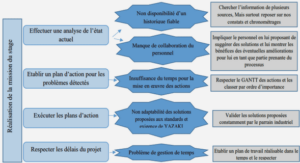
Contributions au théorème central limite et à l’estimation non paramétrique

Processus et champs de variables aléatoires

Nous allons définir rigoureusement la notion de champ de variables aléatoires qui est l’objet principal de notre étude au cours de ce mémoire. Commençons, toutefois, par définir la notion plus générale de processus aléatoire.
Définition 1.1.1 (Processus stochastique). On appelle processus stochastique toute famille de variables aléatoires indexée par un ensemble quelconque non vide T. T est alors appelé ensemble des indices. Les variables aléatoires d’un processus stochastique peuvent être définies sur des espaces de probabilité différents ; cependant, et sauf mention du contraire, toutes les variables aléatoires d’un certain processus stochastique seront définies sur le même espace de probabilité dans la suite. Dans ce mémoire, on parlera de champ de variables aléatoires dès lors que l’ensemble T sera muni d’une loi de composition interne (l.c.i.). Une classe de processus stochastiques particulière qui nous intéressera de par sa proximité avec les champs de variables aléatoires est celle des tableaux triangulaires.
Définition 1.1.2 (Tableau triangulaire). Soient ((Ωn, Fn, µn))n>1 des espaces probabilisés, (kn)n>1 une suite d’entiers et Xn,i, n > 1, i ∈ J1, nK des variables aléatoires telles que pour tout n > 1 et pour tout i ∈ J1, knK, la variable aléatoire Xn,i est définie sur (Ωn, Fn, µn). La famille (Xn,i) n>1 16i6kn est alors appelée tableau triangulaire.

La méthode des blocs de Bernstein

Utilisée pour la première fois en 1927 par Serge Bernstein [Ber27], la méthode des blocs consiste à séparer les variables aléatoires en « petits » et « grands » blocs. Les petits blocs servent à séparer les grands blocs afin que ces derniers soient faiblement dépendants. Le TCL est alors obtenu en traitant les grands blocs comme des variables faiblement dépendantes et en montrant que la contribution des petits blocs devient négligeable devant celle des grands blocs. En tout, cette méthode se compose de trois étapes : la séparation en blocs (petits et grands), la preuve d’un TCL pour les grands blocs (au travers, par exemple, de méthodes d’approximation) et enfin la preuve de la négligeabilité des petits blocs devant les grands blocs au fur et à mesure que la taille de ces derniers croît.

Estimateurs récursifs à noyau

De nos jours, l’estimation non-paramétrique à noyau est un domaine populaire et bien établi en statistique mais malgré les performances notables des estimateurs à noyau, le problème des données en masse et celui des données acquises en continu posent de nouveaux problèmes. En effet, les nouveaux outils numériques permettent aux statisticiens de collecter des quantités très importantes de données ce qui entraîne des difficultés pour leur analyse surtout lorsque des estimations instantanées sont requises. En raison du fait que les estimateurs récursifs satisfont à une relation de récurrence, ils possèdent l’avantage de pouvoir être mis à jour en temps constant quelque soit le nombre d’observations que l’on a obtenues précédemment. Ceci les oppose à leurs équivalents non-récursifs qui doivent être recalculés entièrement dès que de nouvelles données sont disponibles et permet de réduire le coût de calcul de l’estimateur. Il existe de nombreux résultats concernant les propriétés asymptotiques des estimateurs récursifs de la densité ainsi que de la régression pour des données i.i.d. et fortement mélangeantes. On pourra citer, par exemple, les travaux d’Aboubacar Amiri [Ami12], Xiaohong Chen, Yinxiao Huang et Wei Biao Wu [CHW13], László Györfi et Elias Masry ([GM87], [GM90]), Elias Masry [Mas86], George Roussas et Lanh Tran [RT92], Li Wang et Han-Ying Liang [WL04] et encore d’autres.

Modèle de régression et estimateur de Nadaraya-Watson

Dans ce qui suit, nous nous intéresserons à la normalité asymptotique de cet estimateur dans le cadre de données spatiales dépendantes. On considère N un entier strictement positif et ((Yi, Xi))i∈Zd un champ stationnaire de variables aléatoires à valeurs dans R × R N définies sur l’espace de probabilité (Ω, F, P). Supposons que la loi commune µ des variables aléatoires Xi, i ∈ Zd est absolument continue par rapport à la mesure de Lebesgue sur RN . On note par f une densité (inconnue) de µ. Soit Λn une région finie de Zd et soit (ηi)i∈Zd un champ de variables aléatoires i.i.d. à valeurs dans RN centrées et dont les carrés de leurs normes euclidiennes sont intégrables, que l’on suppose indépendant du champ (Xi)i∈Zd . Le modèle de régression est caractérisé par la relation Yi = R(Xi, ηi) pour tout i ∈ Λn où R est une fonctionnelle inconnue.On pourra citer, notamment, Zudi Lu et Ping Cheng [LC97], Lias Masry et Jianqing Fan [MF97], Peter Robinson [Rob83], George Roussas [Rou88] et bien d’autres références. Dans le cas spatial (i.e. pour d > 2), de nombreuses contributions pour le cas des champs fortement mélangeants furent apportées par Gérard Biau et Benoît Cadre [BC04], Michel Carbon et al. [CFT07], Sophie Dabo-Niang et al. [DNRY11], Sophie Dabo-Niang et Anne-Françoise Yao [DNY07], Mohamed El Machkouri [EM07], Mohamed El Machkouri et Radu Stoica [EMS10], Marc Hallin et al. [HLT04] et Zudi Lu et Xing Chen [LC02 ; LC04]. Le but principal de ce chapitre est de donner des conditions suffisantes simples pour obtenir la normalité asymptotique de l’estimateur de Nadaraya-Watson dans le cadre du mélange fort et de la dépendance faible au sens de Wu. À notre connaissance, les résultats présentés dans la section suivante sont les premiers donnant un théorème central limite (théorème 5.2.2) pour l’estimateur de NadarayaWatson sous les conditions minimales sur le paramètre de fenêtre et pour des données spatiales dépendantes. En particulier, nos résultats améliorent de plusieurs manières le théorème central limite pour l’estimateur de Nadarya-Watson dans le cas spatial établi par Gérard Biau et Benoît Cadre [BC04] (voir les commentaires qui suivent le corollaire 5.2.3 ci-dessous). Ce chapitre est organisé comme suit. Nos résultats principaux sont énoncés dans la partie 5.2 alors que les preuves des résultats principaux et des lemmes intermédiaires sont présentées dans les parties 5.4 et 5.5. Enfin, dans la partie 5.3, nous donnerons une illustration du théorème central limite obtenu dans la partie 5.2.

Le rapport de stage ou le pfe est un document d’analyse, de synthèse et d’évaluation de votre apprentissage, c’est pour cela chatpfe.com propose le téléchargement des modèles complet de projet de fin d’étude, rapport de stage, mémoire, pfe, thèse, pour connaître la méthodologie à avoir et savoir comment construire les parties d’un projet de fin d’étude.

Table des matières

I. Généralités et résultats historiques
1. Théorie des probabilités
1.1. Des généralités probabilistes
1.1.1. Processus et champs de variables aléatoires
1.1.2. Convergence en loi des champs
1.1.3. Différentes méthodes de preuve de la convergence en loi
1.2. Un peu de théorie ergodique
1.2.1. Théorèmes ergodiques
1.2.2. Un résultat clé concernant les TCL
1.3. Processus de Wiener et le principe d’invariance
1.3.1. Processus de Wiener
1.3.2. Espace de Skorohod, tension et principe d’invariance
1.4. Martingales à temps discret
1.4.1. Inégalités classiques de la théorie des martingales
1.4.2. Filtrations commutantes et ortho-martingales
1.5. Conditions de dépendance
1.5.1. m-dépendance
1.5.2. Mélange fort
1.5.3. Dépendance physique au sens de Wu
1.5.4. Condition projective du type Hannan
1.6. Théorèmes quenched
2. Statistique
2.1. Estimateurs non-récursifs à noyau
2.1.1. Estimateurs de la densité
2.1.2. Estimateurs de la régression
2.2. Estimateurs récursifs à noyau
2.2.1. Estimateurs de la densité
2.2.2. Estimateurs de la régression
II. Théorèmes limite quenched
3. Théorèmes centraux limite sous la condition de Hannan
3.1. Champs bi-dimensionnels
3.2. Résultats principaux
3.3. Preuves des résultats
3.3.1. Preuve du théorème 3.2.2
3.3.2. Preuve du corollaire 3.2.3 et du théorème 3.2.4
3.4. Champs d-dimensionnels : d > 3
3.4.1. Preuve du théorème 3.4.2 et de ses corollaires
3.5. Exemples
3.5.1. Champ linéaire
3.5.2. Champ de Volterra
4. Théorèmes centraux limite fonctionnels quenched sous la condition de Hannan
4.1. Décomposition martingale-cobord multi-dimensionnelle
4.2. Résultats principaux
4.3. Preuves des résultats
4.3.1. Preuve de la proposition 4.2.1
4.3.2. Preuve du théorème 4.2.2
4.4. Extension aux champs d-dimensionnels, d > 3
4.5. Exemples
4.5.1. Champ linéaire
4.5.2. Champ de Volterra
4.6. Extension des résultats aux espaces d’Orlicz
4.6.1. Théorème central limite fonctionnel sur des régions cubiques
4.6.2. Théorème central limite fonctionnel sur des régions rectangulaires
4.7. Preuves des généralisations
4.7.1. Preuve du lemme principal et du théorème 4.6.4
4.7.2. Preuve du lemme 4.7.2
4.7.3. Conjectures
4.8. Exemples 6
4.8.1. Champ linéaire
4.8.2. Champ de Volterra
III. Estimateurs à noyau
5. Estimateur à noyau de la régression de Nadaraya-Watson pour des données spatiales
5.1. Modèle de régression et estimateur de Nadaraya-Watson
5.2. Résultats principaux
5.2.1. Biais asymptotiques
5.2.2. Normalité asymptotique
5.3. Illustrations numériques
5.4. Lemmes préliminaires
5.4.1. Proposition 5.4.5
5.4.2. Variances et covariance asymptotiques
5.5. Preuves des théorèmes principaux
5.5.1. Preuve du théorème 5.2.1
5.5.2. Preuve du théorème 5.2.2
6. Estimateurs récursifs à noyau pour des données spatiales
6.1. Modèle statistique et estimateurs étudiés
6.2. Résultats principaux
6.2.1. Biais et variance asymptotiques
6.2.2. Normalité asymptotique
6.3. Lemmes préliminaires
6.3.1. Proposition 6.3.7
6.3.2. Proposition 6.3.8
6.4. Preuves des résultats principaux
6.4.1. Preuve de la proposition 6.2.2
6.4.2. Preuve du théorème 6.2.3
6.4.3. Preuve du théorème 6.2.4
Bibliographie