Bilans énergétiques des écoulements permanant

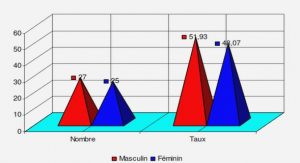
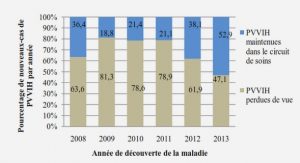
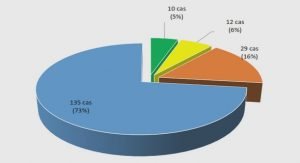
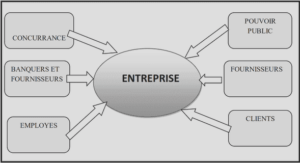
Télécharger le fichier pdf d’un mémoire de fin d’études

ROTOR D’UN HELICOPTERE

Introduction

La mécanique du vol de l’hélicoptère est une science qui vise à établir la théorie du vol des aéronefs à voilure tournante. Elle basée particulièrement sur le fonctionnement du ou des rotor(s).Vu ce sont eux qui caractérisent ce type d’aéronef. La théorie aérodynamique du rotor de l’hélicoptère est fondée sur deux théories, la théorie de Rankine-Froude et la théorie des éléments de pale. Pour une géométrie et une vitesse de rotation données du rotor, et pour une masse connue à sustenter, ces deux théories permettent d’indiquer la puissance sur l’arbre rotor et les pas de pales nécessaires aux différents régimes de vol.

La théorie de Rankine-Froude

Cette théorie est une formulation mathématique de la physique des hélices basée sur la variation de la quantité de mouvement. Elle s’applique aussi bien aux rotors d’hélicoptères, aux hélices marines et aériennes qu’aux éoliennes et hydroliennes. Par hypothèse, on considère l’hélice comme un disque uniforme. Ce disque apparaît comme une hélice possédant une infinité de pales d’épaisseur infiniment petite. De plus, on considère que :
• L’écoulement est irrotationnel.
• Le fluide est incompressible.
• Le disque hélice ne provoque pas de tourbillon hélicoïdal de sillage.
• Le flux est strictement axial et uniforme sur toute la surface du disque hélice ainsi que dans toute section de la veine fluide. Le flux est donc unidirectionnel.
• Les forces de friction sont négligées.

Descriptions

Elle est fondée sur la réalisation d’une force de soulèvement par la génération d’un changement de quantité de mouvement. On suppose l’existence d’un tube d’écoulement (ou Veine fluide) qui est une surface à symétrie axiale passant par le périmètre du disque du rotor Figure 2.01. L’air est supposé incompressible et donc le flux passant en toute section transversale du tube d’écoulement est constante. Cela signifie également qu’à cause des flux unidimensionnel, l’écoulement doit rester dans le même sens pour la plupart des conditions de vol approprié.
Toutefois, cela ne détériore pas le modèle théorique sous certaines conditions de vol.
L’écoulement pénètre dans le tube d’écoulement, est accéléré à travers le disque de rotor, ensuite elle s’épuisé au fond de ce dernier. Loin en amont du disque, l’écoulement vertical de la vitesse doit tendre vers zéro faisant du tube d’écoulement une section de taille infinie. Cependant le tube d’écoulement s’établit et passe à travers le contour du disque de rotor. La vitesse supplémentaire passant à traverslerotorest connue commelavitesse induite. Par la suite elle forme finalement une augmentation de la vitesse de . La force de poussée du rotor, T, peut être évaluée en considérant l’augmentation de la quantité de mouvement. La continuité de l’écoulement à travers la veine fluide nous permet d’écrire l’équation (2.1).
Avec
: la masse volumique de l’air
: l’aire du dique du rotor
: la vitesse induite
: l’aire de la veine fluide considéré
: la vitesse d’écoulement du fluide sur la section
Figure 2.01 : Illustration du tube d’écoulement [SED.11]
La poussée du rotor, due à la variation de la quantité de mouvement, s’exprime comme suit: Chaque seconde un paquet de fluide pénètre dans le tube d’écoulement avec une vitesse verticale nulle. De même, un paquet égal de fluide quitte le tube d’écoulement avec une vitesse verticale de . Par conséquent, dans chaque seconde, il ya production d’une impulsion donnée par l’équation (2.02).
Afin de générer une poussée, il doit y avoir une différence de pression discontinue, de plus le disque du rotor doit présenter une épaisseur nulle. Cependant, le flux d’air à travers le rotor est continu. Nous avons donc la formule suivante :
Où :
: la pression du fluide en aval
: la pression du fluide en amont
La dernière considération est l’application de l’équation de Bernoulli. Cette équation peut être appliquée à l’écoulement en amont ou en aval du disque de rotor, mais pas à travers elle.
Ceci montre que la vitesse induite dépend explicitement de la charge surfacique du disque .
A première vue, tout ceci semble indiquer que, plus la charge surfacique du disque est grande, plus la vitesse induite augmente.
Par conséquent, la puissance nécessaire à l’accélération du fluide est donnés par:
Avec : puissance induite
La puissance induite est la majeure partie de la puissance totale absorbée par un rotor en vol stationnaire. Ce pendant un autre composant de puissance est nécessaire pour surmonter la traînée aérodynamique des pales. C’est la puissance du profil. Etant donné que c’est la puissance induite qui est la fonction utile du rotor, en effet elle produit l’ascension, le rapport de la puissance induite et de la puissance totale fournit une mesure de l’efficacité du rotor en vol stationnaire. Ce rapport est appelé le facteur de mérite, couramment désigné par M.
Par la suite, afin d’évaluer le rendement du rotor et de comparer différents rotors, nous allons recourir aux quantités adimensionnelles. La vitesse induite est normalisé en utilisant la vitesse de pointe du rotor . La vitesse varie le long de l’ensemble des pales du rotor mais la vitesse de pointe est la valeur de définition. Dans les termes de voilure fixe ce problème ne se pose pas, puisque toute l’aile a la même vitesse. La vitesse induite adimensionnelle ce définit ainsi: Où exprime la vitesse de pointe du rotor (vitesse tangentielle des pales)
La force de poussée est également normalisée d’une manière très proche de celle utilisée pour l’ascenseur à voilure fixe. C’est à dire le produit d’une pression et d’un espace. La pression est la pression dynamique aux extrémités des pales du rotor (en vol stationnaire) et la surface est la surface totale du disque. Le coefficient de pression est alors défini par:
Pour un rotor donné lame le coefficient de traînée, et donc la puissance de profil, peuvent être devrait pas varier considérablement avec le niveau de poussée, à condition que les lames ne stagnent pas, ni l’expérience de haute compressibilité glisser hausse. L’équation (2.14) montre que la valeur de M, pour un rotor donné, augmente généralement avec l’accroissement .Cette fonctionnalité signifie que la prudence s’impose dans l’utilisation de la figure de mérite à des fins de comparaison. Un concepteur peut avoir une portée pour produire une valeur élevée de Men sélectionnant une hélice de petite section, vue que les lames fonctionnent à un coefficient de portance élevée, proche du décrochage, mais ils ont besoin pour être sûr que la surface de la pale ai une distance suffisante pour que les conditions de vol stationnaire soient satisfaite. Une comparaison des différents modèles d’hélice pour une application donnée doit être faite à un coefficient de poussée constante.

Modélisation du tube d’écoulement

Afin d’étudier le concept, le tube d’écoulement doit être modélisé. La variation de la vitesse peut être exprimée comme suit : [SED.11]
– s est la variable de position verticale avec l’origine au centre du disque de rotor dans le sens positif vers le bas;
– h est une distance définissant l’étendue du tube d’écoulement,
– k est un facteur d’ajustement l’intensité de la contraction.
Après avoir défini la variation de la vitesse, on détermine la variation de pression qui le saut de pression à disque référencée à chaque extrémité du tube d’écoulement, lors du retour de pression
à l’air ambiante. Ainsi, en utilisant l’équation de Bernoulli,

Table des matières

INTRODUCTION GENERALE
CHAPITRE 1 ETAT DE L’ART SUR L’AERONAUTIQUE
1.1 Introduction
1.2 Historique
1.3 Mécanique des fluides
1.3.1 Généralité
1.3.2 Hydrostatiques
1.3.3 Cinématique des fluides
1.3.4 Dynamique des fluides
1.3.5 Bilans énergétiques des écoulements permanant
1.3.6 Théorème d’Euler
1.4 Conclusion
CHAPITRE 2 ROTOR D’UN HELICOPTERE
2.1 Introduction
2.2 La théorie de Rankine-Froude
2.2.1 Descriptions
2.2.2 Modélisation du tube d’écoulement
2.2.3 Vol Axial
2.3 Théorie des éléments de la pale
2.3.1 Méthode de base
2.3.2 Phénomène de portance et d’aspiration
2.3.3 Propriétés de la voilure
2.3.4 Propriétés des pales
2.3.5 Approximations de la poussée
2.3.6 Rotor en vol en avant
2.4 Conclusion
CHAPITRE 3 MODÉLISATION DE LA DYNAMIQUE DE VOL DE L’HÉLICOPTÈRE
3.1 Introduction
3.2 Principe du vol de l’hélicoptère
3.2.1 Description de l’hélicoptère
3.2.2 Principe de propulsion
3.2.3 Principe de commandes
3.3 Hypothèses et simplifications
3.4 Construction du modèle
3.4.2 Produits et moments d’inerties
3.4.3 Equations de mouvement
3.4.4 Forces et moment
3.5 Conclusions
CHAPITRE 4 SIMULATION
4.1 Introduction
4.2 Linéarisation des équations de mouvement
4.3 Caractéristiques de l’hélicoptère
4.4 Etude de la stabilité du système
4.5 Correction du système par LQ
4.5.1 Méthode LQ
4.5.2 Méthode LQG
4.5.3 Méthode LQG/LTR
4.6 Correction du système
4.7 Simulation
4.8 Résultats et discussions
4.9 Conclusion
CONCLUSION GENERALE
BIBLIOGRAPHIE
WEBOGRAPHIE
ANNEXES

Télécharger le rapport complet