Object-oriented Languages
Object-oriented languages provide the language support for the object-oriented paradigm. A programming language is said to be object-oriented if it satisfies the three properties of encapsulation, inheritance and polymorphism. Roughly speaking, encapsulations facilitates code modularization, inheritance make possible code sharing and polymorphism enables to call a variety of functions using exactly the same interface. More specifically,
– encapsulation means that the state of an object is not directly accessible by the context. This implies that the only way to access to object data is through messages passing;
– inheritance allows to create objects by specializing or redefining existing ones. The inherited object may answer to all the messages of the parent;
– polymorphism means that the same operation may behave differently on objects of different classes. There are two main families of object-oriented languages. The first family contains object-oriented extensions of procedural or functional languages such as C++ [101], Objective-C [5], Object Pascal [12] or OCAML [70]. The advantage of such languages is that they are backwardcompatible with existing code, so that they favor a smoothly migration to object-oriented. The drawback is that as they are half path languages they present some idiosyncrasies, e.g. rather complicated syntax and semantics.
The second family contains pure object-oriented languages as Smalltalk [55], Java [56] or C# [84]. The advantage of such languages is that they strongly enroll the object-oriented concepts, so that for instance they ensure encapsulation. The drawback is that they oblige the programmer to work following the object-oriented methodology. In mainstream languages of both families, objects are intensionally described by classes. A class is a description of the structure and the behavior of set of objects. Classes may specify access permissions for clients and inherited classes, visibility and member lookup resolution. Objects are created through class instantiation.
Verification and Optimization
Verification of object-oriented programs is a hard task made harder by some peculiarities of such languages as inheritance, virtual methods and componentbased development. Traditional program testing has two drawbacks. First, it is not sound as just a finite number of executions can be covered. Second, the testing of a class is made even harder by the fact that the instantiation context is not known a priori. Theorem provers require heavy human interactions, and even for rather simple cases they may entail a considerable human effort, e.g. as in [60]. As a consequence they are not suited for the analysis of large programs. Model checkers suffer of the state-explosion problem, the incapability of checking directly the source code and the limitations to adapt to modules without human-provided annotations [65]. Optimization is a sensible issue in the implementation of object-oriented languages. Dynamic resolutions of method-calls [42], implicit box and unboxing of objects [89], checks of array bounds [3], etc. may cause nonnegligible slowdown. Nevertheless, most of the existing optimizations are whole-program, so that e.g. they cannot be used for the optimization of a single class, aside from its context.
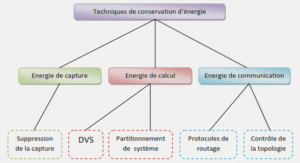
Modularity
Modular reasoning is a widespread methodology that has been proved effective in many human activities. It enables to handle complex problems by studying smaller, easier to deal with sub-problems, connected by a simple structure, and independent enough to allow further work to proceed separately on each of them. In computer science it is a main tool for reasoning about parts of the systems, develop components independently, and even configure customized systems. For instance, it has been worthwhile for system designs, as a methodology to specify and to document the artifacts of a system under development [97]; for language specification as constructs capable to express and to check some aspects of the modular structure [69]; for compilation as a way to structure the source code and to speed-up the compiling process [17]. A methodology is worthy of being called modular if it satisfies at least the three requirements of decomposability, composability and understandability. We say that a methodology satisfies
– the decomposability requirement if it allows to decompose a complex task into easier sub-problems, connected by a simple structure and mutually independent;
– the composability requirement if it favors the production of elements which may be freely combined with each other to produce new systems;
– the understandability requirement if the elements can be understood with a limited knowledge of the others.
The object-oriented paradigm satisfies the requirements above. In such a view a complex system is decomposed into a set of objects which interact via message passing. Objects are specified and developed independently, so that it is possible to reuse them in contexts different from the one they were originally designed for. Finally, objects have a clear interface, i.e. the messages they can answer, so that they can be understood without a full knowledge of the surrounding context.
Abstract Interpretation
We use the theoretical framework of Abstract Interpretation. Abstract Interpretation is a general theory due to P. Cousot’s thèse ès sciences mathématiques [25] which formalizes the notion of approximation. In particular, it formalizes the idea that the semantics of a language can be more or less precise depending on the considered observation level. Semantics can be partially ordered according to their relative precision [29, 28] and the more precise the semantics the more precise the properties about programs it captures. An abstract interpretation-based static analysis is an abstract semantics which is precise enough to capture properties of interest and coarse enough to be computable. Differently stated, a static analysis is a sound, finite and approximate calculation of the program semantics. Those three requirements imply that
– no program behavior is ignored (soundness);
– the static analysis terminates and the inferred property is computerrepresentable (finiteness);
– the inferred property may not be the most precise one (approximation).
|
Table des matières
1 Introduction
1.1 Motivations
1.1.1 Object-oriented Languages
1.1.2 Verification and Optimization
1.1.3 Modularity
1.2 Abstract Interpretation
1.3 Results
1.3.1 Static Analysis of Classes
1.3.2 Introductory Example
1.3.3 Main Results
1.4 Overview of the Thesis
2 Preliminaries
2.1 Notation and Basic Definitions
2.1.1 Partial Orders
2.1.2 Functions and Fixpoints
2.1.3 Traces
2.2 Abstract Interpretation
2.2.1 Galois Connections
2.2.2 Fixpoint Approximation
2.2.3 Chaotic and Asynchronous Iterations
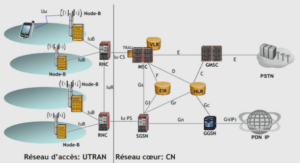
3 Concrete Semantics
3.1 Semantics of Object-oriented Languages in Literature
3.1.1 Types
3.1.2 Object Calculi
3.1.3 Abstract State Machines
3.1.4 Denotational Semantics
3.2 Whole-Program Trace Semantics
3.2.1 Syntax
3.2.2 Semantic Domains
3.2.3 Whole-Program Semantics
3.3 Class Trace Semantics
3.3.1 Constructor and Methods Semantics
3.3.2 Object Semantics
3.3.3 Class Semantics
3.4 Relation between wJ·K and cJ·K
3.4.1 Abstraction
3.4.2 Soundness and Completeness of the Class Semantics
3.5 Languages with Class Destructor
4 Abstract Semantics
4.1 Stepwise Abstraction
4.2 First Abstraction: Collecting Traces
4.2.1 Abstract Domain
4.2.2 Abstraction
4.2.3 Abstract Semantics
4.3 Second Abstraction: Reachable States
4.3.1 Abstract Domain
4.3.2 Abstraction
4.3.3 Abstract Semantics
5 Inference of Class Invariants
6 Symbolic Relations for the Approximation of Set of Traces
7 Symbolic Relations for Approximating the Class Semantics
8 Class Invariants in Presence of Inheritance
9 Static Analysis-based Inheritance
10 Context Approximation
11 Conclusions
![]() Télécharger le rapport complet
Télécharger le rapport complet